Advertisements
Advertisements
प्रश्न
In a diatomic molecule, the rotational energy at a given temperature ______.
- obeys Maxwell’s distribution.
- have the same value for all molecules.
- equals the translational kinetic energy for each molecule.
- is (2/3)rd the translational kinetic energy for each molecule.
उत्तर
a and d
Explanation:
Consider a diatomic molecule as shown in the diagram.
The total energy associated with the molecule is
`E = 1/2 mv_x^2 + 1/2 mv_y^2 + 1/2 mv_z^2 + 1/2 I_xω_x^2 + 1/2 I_yω_y^2`
This above expression contains translational kinetic energy `(1/2 mv^2)` corresponding to velocity in each x, y and z-directions as well as rotational KE `(1/2 Iω^2)` associated with the axis of rotations x and y.
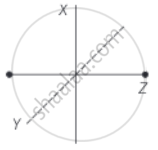
The number of independent terms in the above expression is 5.
As we can predict the velocities of molecules by Maxwell's distribution, hence the above expression also obeys Maxwell's distribution.
∵ 2 rotational and 3 translational energies are associated with each molecule.
∴ Rational energy at a given temperature is `(2/3)`rd of translational KE of each molecule.
APPEARS IN
संबंधित प्रश्न
The energy of a given sample of an ideal gas depends only on its
The average momentum of a molecule in a sample of an ideal gas depends on
A sample of 0.177 g of an ideal gas occupies 1000 cm3 at STP. Calculate the rms speed of the gas molecules.
The ratio of the molar heat capacities of an ideal gas is Cp/Cv = 7/6. Calculate the change in internal energy of 1.0 mole of the gas when its temperature is raised by 50 K (a) keeping the pressure constant (b) keeping the volume constant and (c) adiaba
Two ideal gases have the same value of Cp / Cv = γ. What will be the value of this ratio for a mixture of the two gases in the ratio 1 : 2?
An ideal gas at pressure 2.5 × 105 Pa and temperature 300 K occupies 100 cc. It is adiabatically compressed to half its original volume. Calculate (a) the final pressure (b) the final temperature and (c) the work done by the gas in the process. Take γ = 1.5
An ideal gas of density 1.7 × 10−3 g cm−3 at a pressure of 1.5 × 105 Pa is filled in a Kundt's tube. When the gas is resonated at a frequency of 3.0 kHz, nodes are formed at a separation of 6.0 cm. Calculate the molar heat capacities Cp and Cv of the gas.
When an ideal gas is compressed adiabatically, its temperature rises: the molecules on the average have more kinetic energy than before. The kinetic energy increases ______.
- because of collisions with moving parts of the wall only.
- because of collisions with the entire wall.
- because the molecules gets accelerated in their motion inside the volume.
- because of redistribution of energy amongst the molecules.
The container shown in figure has two chambers, separated by a partition, of volumes V1 = 2.0 litre and V2 = 3.0 litre. The chambers contain µ1 = 4.0 and µ2 = 5.0 moles of a gas at pressures p1 = 1.00 atm and p2 = 2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.
| V1 | V2 |
| µ1, p1 | µ2 |
| p2 |
We have 0.5 g of hydrogen gas in a cubic chamber of size 3 cm kept at NTP. The gas in the chamber is compressed keeping the temperature constant till a final pressure of 100 atm. Is one justified in assuming the ideal gas law, in the final state?
(Hydrogen molecules can be consider as spheres of radius 1 Å).
