Advertisements
Advertisements
प्रश्न
In a diatomic molecule, the rotational energy at a given temperature ______.
- obeys Maxwell’s distribution.
- have the same value for all molecules.
- equals the translational kinetic energy for each molecule.
- is (2/3)rd the translational kinetic energy for each molecule.
उत्तर
a and d
Explanation:
Consider a diatomic molecule as shown in the diagram.
The total energy associated with the molecule is
`E = 1/2 mv_x^2 + 1/2 mv_y^2 + 1/2 mv_z^2 + 1/2 I_xω_x^2 + 1/2 I_yω_y^2`
This above expression contains translational kinetic energy `(1/2 mv^2)` corresponding to velocity in each x, y and z-directions as well as rotational KE `(1/2 Iω^2)` associated with the axis of rotations x and y.
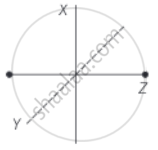
The number of independent terms in the above expression is 5.
As we can predict the velocities of molecules by Maxwell's distribution, hence the above expression also obeys Maxwell's distribution.
∵ 2 rotational and 3 translational energies are associated with each molecule.
∴ Rational energy at a given temperature is `(2/3)`rd of translational KE of each molecule.
APPEARS IN
संबंधित प्रश्न
Keeping the number of moles, volume and temperature the same, which of the following are the same for all ideal gases?
The average momentum of a molecule in a sample of an ideal gas depends on
Let Q and W denote the amount of heat given to an ideal gas and the work done by it in an isothermal process.
An amount Q of heat is added to a monatomic ideal gas in a process in which the gas performs a work Q/2 on its surrounding. Find the molar heat capacity for the process
An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p = kV. Show that the molar heat capacity of the gas for the process is given by `"C" ="C"_"v" +"R"/2.`
The volume of an ideal gas (γ = 1.5) is changed adiabatically from 4.00 litres to 3.00 litres. Find the ratio of (a) the final pressure to the initial pressure and (b) the final temperature to the initial temperature.
An ideal gas at pressure 2.5 × 105 Pa and temperature 300 K occupies 100 cc. It is adiabatically compressed to half its original volume. Calculate (a) the final pressure (b) the final temperature and (c) the work done by the gas in the process. Take γ = 1.5
Consider a given sample of an ideal gas (Cp/Cv = γ) having initial pressure p0 and volume V0. (a) The gas is isothermally taken to a pressure p0/2 and from there, adiabatically to a pressure p0/4. Find the final volume. (b) The gas is brought back to its initial state. It is adiabatically taken to a pressure p0/2 and from there, isothermally to a pressure p0/4. Find the final volume.
Two vessels A and B of equal volume V0 are connected by a narrow tube that can be closed by a valve. The vessels are fitted with pistons that can be moved to change the volumes. Initially, the valve is open and the vessels contain an ideal gas (Cp/Cv = γ) at atmospheric pressure p0 and atmospheric temperature T0. The walls of vessel A are diathermic and those of B are adiabatic. The valve is now closed and the pistons are slowly pulled out to increase the volumes of the vessels to double the original value. (a) Find the temperatures and pressures in the two vessels. (b) The valve is now opened for sufficient time so that the gases acquire a common temperature and pressure. Find the new values of the temperature and pressure.
ABCDEFGH is a hollow cube made of an insulator (Figure). Face ABCD has positive charge on it. Inside the cube, we have ionized hydrogen. The usual kinetic theory expression for pressure ______.
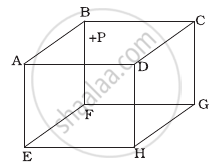
- will be valid.
- will not be valid since the ions would experience forces other than due to collisions with the walls.
- will not be valid since collisions with walls would not be elastic.
- will not be valid because isotropy is lost.
