Advertisements
Advertisements
प्रश्न
Diatomic molecules like hydrogen have energies due to both translational as well as rotational motion. From the equation in kinetic theory `pV = 2/3` E, E is ______.
- the total energy per unit volume.
- only the translational part of energy because rotational energy is very small compared to the translational energy.
- only the translational part of the energy because during collisions with the wall pressure relates to change in linear momentum.
- the translational part of the energy because rotational energies of molecules can be of either sign and its average over all the molecules is zero.
उत्तर
c
Explanation:
According to kinetic theory. we assume the walls only exert perpendicular forces on molecules. They do not exert any parallel force. hence there will not be any type of rotation present.
The wall produces one change in translational motion.
Hence, in the equation
`pV = 2/3 E` .....`[(Where P = pressure),(V = Volume)]`
E is representing only the translational part of energy.
APPEARS IN
संबंधित प्रश्न
Consider the quantity \[\frac{MkT}{pV}\] of an ideal gas where M is the mass of the gas. It depends on the
Let Q and W denote the amount of heat given to an ideal gas and the work done by it in an adiabatic process.
(a) Q = 0
(b) W = 0
(c) Q = W
(d) Q ≠ W
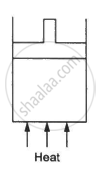
The figure shows a cylindrical container containing oxygen (γ = 1.4) and closed by a 50-kg frictionless piston. The area of cross-section is 100 cm2, atmospheric pressure is 100 kPa and g is 10 m s−2. The cylinder is slowly heated for some time. Find the amount of heat supplied to the gas if the piston moves out through a distance of 20 cm.
An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p = kV. Show that the molar heat capacity of the gas for the process is given by `"C" ="C"_"v" +"R"/2.`
Two ideal gases have the same value of Cp / Cv = γ. What will be the value of this ratio for a mixture of the two gases in the ratio 1 : 2?
Two samples A and B, of the same gas have equal volumes and pressures. The gas in sample A is expanded isothermally to double its volume and the gas in B is expanded adiabatically to double its volume. If the work done by the gas is the same for the two cases, show that γ satisfies the equation 1 − 21−γ = (γ − 1) ln2.
An ideal gas of density 1.7 × 10−3 g cm−3 at a pressure of 1.5 × 105 Pa is filled in a Kundt's tube. When the gas is resonated at a frequency of 3.0 kHz, nodes are formed at a separation of 6.0 cm. Calculate the molar heat capacities Cp and Cv of the gas.
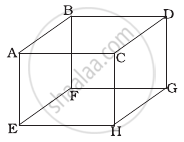
1 mole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K (Figure). One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it. At any given time ______.
ABCDEFGH is a hollow cube made of an insulator (Figure). Face ABCD has positive charge on it. Inside the cube, we have ionized hydrogen. The usual kinetic theory expression for pressure ______.
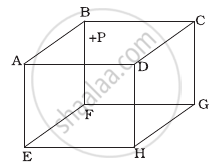
- will be valid.
- will not be valid since the ions would experience forces other than due to collisions with the walls.
- will not be valid since collisions with walls would not be elastic.
- will not be valid because isotropy is lost.
In a diatomic molecule, the rotational energy at a given temperature ______.
- obeys Maxwell’s distribution.
- have the same value for all molecules.
- equals the translational kinetic energy for each molecule.
- is (2/3)rd the translational kinetic energy for each molecule.
