Advertisements
Advertisements
प्रश्न
Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
विकल्प
True
False
उत्तर
This statement is True.
Explanation:
All attempts to prove the fifth postulate as a theorem led to a great achievement in the creation of several other geometries. These geometries are quite different from Euclidean geometry and called non-Euclidean geometry.
APPEARS IN
संबंधित प्रश्न
If a point C lies between two points A and B such that AC = BC, then prove that AC = `1/2` AB. Explain by drawing the figure.
The total number of propositions in the Elements are ______.
In ancient India, the shapes of altars used for household rituals were ______.
In Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for ______.
Euclid stated that all right angles are equal to each other in the form of ______.
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.
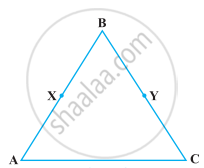
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have BX = `1/2` AB, BY = `1/2` BC and AB = BC. Show that BX = BY.
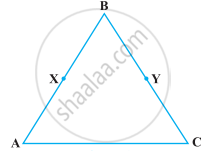
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AC = DC, CB = CE. Show that AB = DE.
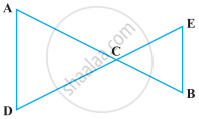
Read the following two statements which are taken as axioms:
- If two lines intersect each other, then the vertically opposite angles are not equal.
- If a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°.
Is this system of axioms consistent? Justify your answer.
Read the following axioms:
- Things which are equal to the same thing are equal to one another.
- If equals are added to equals, the wholes are equal.
- Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
