Question

बिंदुओं A(1, 5) और B(4, 6) को मिलाने वाले रेखाखंड का लंब समद्वि भाजक y-अक्ष को निम्नलिखित बिंदु पर काटता ______ हैं।

विकल्प

• (0, 13)

• (0, –13)

• (0, 12)

• (13, 0)

Answer 1

बिंदुओं A(1, 5) और B(4, 6) को मिलाने वाले रेखाखंड का लंब समद्वि भाजक y-अक्ष को निम्नलिखित बिंदु पर काटता (0, 13) हैं।

स्पष्टीकरण:

सबसे पहले, हम कागज पर लाइन सेगमेंट के बिंदुओं को प्लॉट करते हैं और उनके साथ जुड़ते हैं।

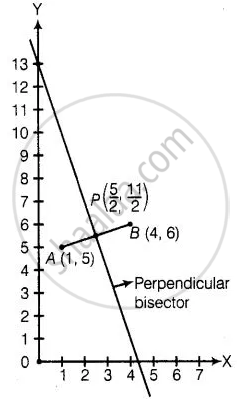
हम जानते हैं कि, लाइन सेगमेंट के लंबवत द्विभाजक एबी सेगमेंट एबी को काटते हैं, अर्थात्, लाइन सेगमेंट एबी के लंबवत द्विभाजक एबी के मध्य-बिंदु से गुजरते हैं।

∴ AB का मध्य-बिंदु = `((1 + 4)/2, (5 + 6)/2)`  ...`[∵ "लाइन सेगमेंट का मध्य-बिंदु अंक से गुजरता है"  (x_1, y_1)  "और"  (x_2, y_2) = ((x_1 + x_2)/2, (y_1 + y_2)/2)]`

⇒ P = `(5/2, 11/2)`

अब, हम मिड-पॉइंट पी के माध्यम से पेपर पास पर एक सीधी रेखा खींचते हैं।

हम देखते हैं कि लंबवत द्विभाजक बिंदु (0, 13) पर Y-अक्ष को काटता है।

अतः अभीष्ट बिंदु (0, 13) है।

Answer 2

बिंदुओं A(1, 5) और B(4, 6) को मिलाने वाले रेखाखंड का लंब समद्वि भाजक y-अक्ष को निम्नलिखित बिंदु पर काटता (0, 13) हैं।

स्पष्टीकरण:

हम जानते हैं कि, लाइन का समीकरण जो बिंदुओं (x₁, y₁) और (x₂, y₂) से गुजरता है।

`(y - y_1) = (y_2 - y_1)/(x_2 - x_1) (x - x_1)` ...(i)

यहाँ, x₁ = 1, y₁ = 5 और x₂ = 4, y₂ = 6

तो, अंकों A(1, 5) और B(4, 6) में शामिल होने वाले लाइन सेगमेंट का समीकरण है।

`(y - 5) = (6 - 5)/(4 - 1)(x - 1)`

⇒ `(y - 5) = 1/3(x - 1)`

⇒ `3y - 15 = x - 1`

⇒ `3y = x - 14`

⇒ `y = 1/3x - 14/3`  ...(ii)

∴ लाइन सेगमेंट का ढलान, m₁ = `1/3`

यदि दो लाइनें एक दूसरे के लंबवत हैं, तो इसकी ढलान के बीच का संबंध है।

m₁ · m₂ = – 1  ...(iii)

जहां, m₁ = लाइन का ढलान 1

और m₂ = लाइन 2 का ढलान

इसके अलावा, हम जानते हैं कि लाइन सेगमेंट के लंबवत द्विभाजक लाइन सेगमेंट पर लंबवत है।

चलो लाइन खंड का ढलान m₂ है।

समीकरण (iii) से,

`m_1 * m_2 = 1/3 * m_2` =  – 1

⇒ m₂ = – 3

 हम यह भी जानते हैं कि लंबवत द्विभाजक लाइन सेगमेंट के मध्य-बिंदु से गुजरता है।

∴ लाइन सेगमेंट का मध्य-बिंदु = `((1 + 4)/2, (5 + 6)/2) = (5/2, 1/2)`

लंबवत द्विभाजक का समीकरण, जिसमें ढलान (–3) है और बिंदु `(5/2, 11/2)` से गुजरता है।

`(y - 11/2) = (-3)(x - 5/2)`   ...[चूंकि, लाइन का समीकरण बिंदु (x₁, y₁) से गुजरता है और ढलान m (y – y₁) = m(x – x₁) होता है] 

⇒ (2y – 11) = – 3(2x – 5)

⇒ 2y – 11 = – 6x + 15

⇒ 6x + 2y = 26

⇒ 3x + y = 13   ...(iv)

यदि लंबवत बिसेटर y-अक्ष को काटता है,

फिर x = 0 को समीकरण (iv) में डालें,

3 × 0 + y = 13

⇒ y = 13

तो, आवश्यक बिंदु (0, 13) है।