Advertisements
Advertisements
प्रश्न
Calculate x :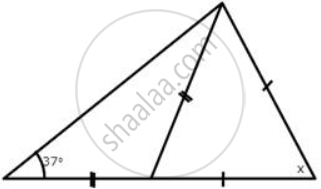
उत्तर
Let the triangle be ABC and the altitude be AD.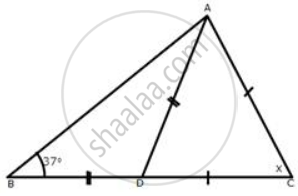
In ΔABD,
∠DBA = ∠DAB = 37° .....[Given BD = AD and angles opposite to equal sides are equal]
Now,
∠CDA = ∠DBA + ∠DAB .......[Exterior angle is equal to the sum of opp. interior angles]
∴ ∠CDA = 37° + 37°
⇒ ∠CDA = 74°
Now in ΔADC,
∠CDA = ∠CAD = 74° ....[ Given CD = AC and angles opposite to equal sides are equal]
Now,
∠CAD + ∠CDA + ∠ACD = 180°
⇒ 74° + 74° + x = 180°
⇒ x = 180° − 148°
⇒ x = 32°
APPEARS IN
संबंधित प्रश्न
An isosceles triangle ABC has AC = BC. CD bisects AB at D and ∠CAB = 55°.
Find:
- ∠DCB
- ∠CBD
In the figure given below, LM = LN; angle PLN = 110o.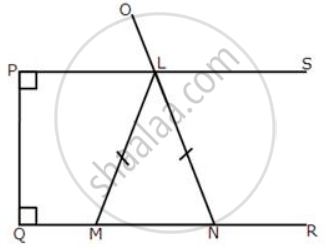
calculate: (i) ∠LMN
(ii) ∠MLN
Calculate x :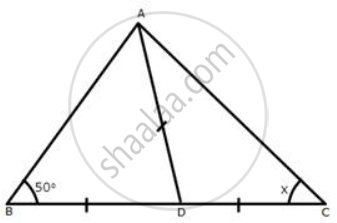
In the given figure; AB = BC and AD = EC.
Prove that: BD = BE.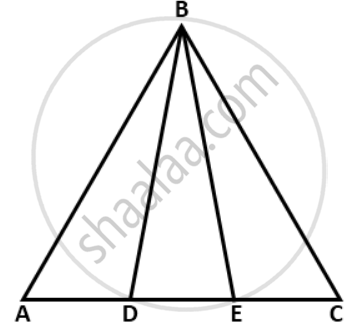
Prove that a triangle ABC is isosceles, if: altitude AD bisects angles BAC.
In the given figure, AD = AB = AC, BD is parallel to CA and angle ACB = 65°. Find angle DAC.
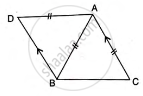
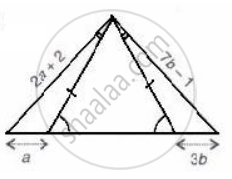
Using the information given of the following figure, find the values of a and b.
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD.
Prove that: ∠BCD = 90°
ABC is a triangle. The bisector of the angle BCA meets AB in X. A point Y lies on CX such that AX = AY.
Prove that: ∠CAY = ∠ABC.
Use the given figure to prove that, AB = AC.
