Advertisements
Advertisements
प्रश्न
Can a Van der Waals gas with a = 0 be liquefied? explain.
उत्तर
- a = 0 for a Van der Waals gas i.e. for a real gas. Van der Waals constant a = 0. It cannot be liquefied.
- If a = 0, there is very less interaction between the molecules of gas.
- ‘a’ is the measure of the strength of Van der Waals force of attraction between the molecules of the gas.
- If a is equal to zero, the Van der Waals force of attraction is very less and the gas cannot be liquefied.
APPEARS IN
संबंधित प्रश्न
Maximum deviation from ideal gas is expected from
Which of the following diagrams correctly describes the behaviour of a fixed mass of an ideal gas? (T is measured in K)
Write the Van der Waals equation for a real gas. Explain the correction term for pressure and volume.
A plot of volume (V) versus temperature (T) for a gas at constant pressure is a straight line passing through the origin. The plots at different values of pressure are shown in Figure. Which of the following order of pressure is correct for this gas?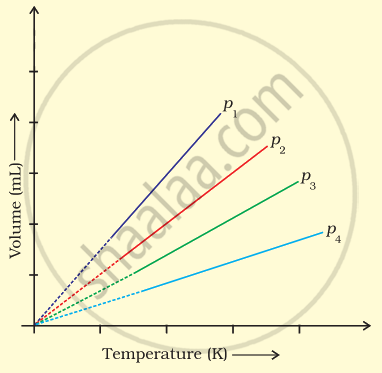
If 1 gram of each of the following gases are taken at STP, which of the gases will occupy (a) greatest volume and (b) smallest volume?
\[\ce{CO, H2O, CH4 , NO}\]
Compressibility factor, Z, of a gas is given as Z = `(pV)/(nRT)`. What is the value of Z for an ideal gas?
Compressibility factor, Z, of a gas is given as Z = `(pV)/(nRT)`. For real gas what will be the effect on value of Z above Boyle’s temperature?
Match the following graphs of ideal gas with their co-ordinates:
| Graphical representation | x and y co-ordinates |
(i)  |
(a) pV vs. V |
(ii) 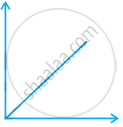 |
(b) p vs. V |
(iii) 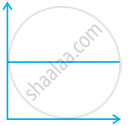 |
(c) p vs. `1/V` |
Assertion (A): At constant temperature, pV vs V plot for real gases is not a straight line.
Reason (R): At high pressure all gases have \[\ce{Z}\] > 1 but at intermediate pressure most gases have \[\ce{Z}\] < 1.
Choose the correct option for the total pressure (in atm.) in a mixture of 4g \[\ce{O2}\] and 2g \[\ce{H2}\] confined in a total volume of one litre at 0°C is ______.
[Given R = 0.082 L atm mol−1K−1, T = 273 K]
