Advertisements
Advertisements
प्रश्न
Suppose there is a tiny sticky area on the wall of a container of gas. Molecules hitting this area stick there permanently. Is the pressure greater or less than on the ordinary area of walls?
उत्तर
- Molecules hitting the tiny sticky area on the wall of the container of gas moves faster as they get closer to the adhesive surface, but this effect is not permanent.
- The pressure on the sticky wall is greater than on the ordinary area of walls.
APPEARS IN
संबंधित प्रश्न
Which of the following diagrams correctly describes the behaviour of a fixed mass of an ideal gas? (T is measured in K)
In what way real gases differ from ideal gases.
Can a Van der Waals gas with a = 0 be liquefied? explain.
Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if it is compressed to a smaller volume at a constant temperature.
Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if the temperature is raised while keeping the volume constant.
Compressibility factor, Z, of a gas is given as Z = `(pV)/(nRT)`. For real gas what will be the effect on value of Z above Boyle’s temperature?
Pressure versus volume graph for a real gas and an ideal gas are shown in figure. Answer the following questions on the basis of this graph.
(i) Interpret the behaviour of real gas with respect to ideal gas at low pressure.
(ii) Interpret the behaviour of real gas with respect to ideal gas at high pressure.
(iii) Mark the pressure and volume by drawing a line at the point where real gas behaves as an ideal gas.
Match the following graphs of ideal gas with their co-ordinates:
| Graphical representation | x and y co-ordinates |
(i)  |
(a) pV vs. V |
(ii) 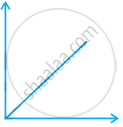 |
(b) p vs. V |
(iii) 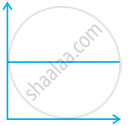 |
(c) p vs. `1/V` |
Isotherms of carbon dioxide gas are shown in figure. Mark a path for changing gas into liquid such that only one phase (i.e., either a gas or a liquid) exists at any time during the change. Explain how the temperature, volume and pressure should be changed to carry out the change.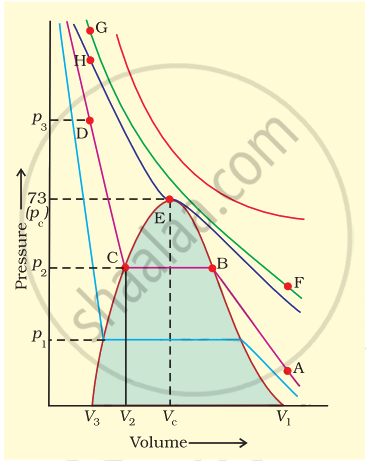
In van der Waal's equation for the real gas, the expression for the net force of attraction amongst the gas molecules is given by:
