Advertisements
Advertisements
प्रश्न
Compare resistance and reactance.
उत्तर
- Resistance:
- Resistance is opposition to the flow of charges (current) and appears in a DC circuit as well as in an AC circuit.
- In a purely resistive circuit, current and voltage are always in phase.
- Resistance does not depend on the frequency of AC.
- Resistance gives rise to the production of Joule heat in a component.
- Reactance:
- The term reactance appears only in an AC circuit. It occurs when an inductor and/or a capacitor are used.
- When reactance is not zero, there is nonzero phase difference between current and voltage.
- Reactance depends on the frequency of AC. In the case of an inductor, reactance increases linearly with frequency. In the case of a capacitor, reactance decreases as the frequency of AC increases; it is inversely proportional to frequency.
- In a circuit with pure reactance, there is no production of heat.
APPEARS IN
संबंधित प्रश्न
Show that the current leads the voltage in phase by π/2 in an AC circuit containing an ideal capacitor ?
When an AC source is connected to a capacitor, there is a steady-state current in the circuit. Does it mean that the charges jump from one plate to the other to complete the circuit?
A current i1 = i0 sin ωt passes through a resistor of resistance R. How much thermal energy is produced in one time period? A current i2 = −i0 sin ωt passes through the resistor. How much thermal energy is produced in one time period? If i1 and i2 both pass through the resistor simultaneously, how much thermal energy is produced? Is the principle of superposition obeyed in this case?
Is energy produced when a transformer steps up the voltage?
A transformer is designed to convert an AC voltage of 220 V to an AC voltage of 12 V. If the input terminals are connected to a DC voltage of 220 V, the transformer usually burns. Explain.
An AC source producing emf ε = ε0 [cos (100 π s−1)t + cos (500 π s−1)t] is connected in series with a capacitor and a resistor. The steady-state current in the circuit is found to be i = i1 cos [(100 π s−1)t + φ1) + i2 cos [(500π s−1)t + ϕ2]. So,
A bulb rated 60 W at 220 V is connected across a household supply of alternating voltage of 220 V. Calculate the maximum instantaneous current through the filament.
The dielectric strength of air is 3.0 × 106 V/m. A parallel-plate air-capacitor has area 20 cm2 and plate separation 0.10 mm. Find the maximum rms voltage of an AC source that can be safely connected to this capacitor.
Suppose the initial charge on the capacitor is 6 mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
If circuit containing capacitance only, the current ______.
A.C. power is transmitted from a power house at a high voltage as ______.
When an ac voltage of 220 V is applied to the capacitor C, then ______.
A capacitor has capacitance C and reactance X, if capacitance and frequency become double, then reactance will be ______.
When an AC voltage of 220 V is applied to the capacitor C ______.
- the maximum voltage between plates is 220 V.
- the current is in phase with the applied voltage.
- the charge on the plates is in phase with the applied voltage.
- power delivered to the capacitor is zero.
Explain why the reactance provided by a capacitor to an alternating current decreases with increasing frequency.
In the LCR circuit shown in figure, the ac driving voltage is v = vm sin ωt.
- Write down the equation of motion for q (t).
- At t = t0, the voltage source stops and R is short circuited. Now write down how much energy is stored in each of L and C.
- Describe subsequent motion of charges.
Define Capacitive reactance.
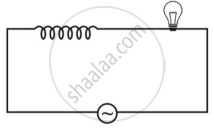
An iron cored coil is connected in series with an electric bulb with an AC source as shown in figure. When iron piece is taken out of the coil, the brightness of the bulb will ______.
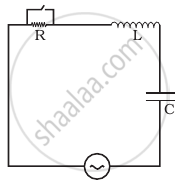
A resistor of 50 Ω, a capacitor of `(25/pi)` µF and an inductor of `(4/pi)` H are connected in series across an ac source whose voltage (in volts) is given by V = 70 sin (100 πt). Calculate:
- the net reactance of the circuit
- the impedance of the circuit
- the effective value of current in the circuit.
