Advertisements
Advertisements
प्रश्न
Consider two ‘postulates’ given below:-
- Given any two distinct points A and B, there exists a third point C which is in between A and B.
- There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
उत्तर
Yes, these postulates include undefined terms like 'point and line'. Furthermore, these postulates are consistent because they deal with two distinct situations:
- States that given two points, A and B, a point C exists on the line that connects them. Whereas
- States that given points A and B, you can select a point C that is not on the line that connects them.
No, these postulates are not derived from Euclid's postulates but rather from the axiom, "Given two distinct points, there is a unique line that passes through them."
APPEARS IN
संबंधित प्रश्न
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
parallel lines
Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
In how many points two distinct lines can intersect?
Given three distinct points in a plane, how many lines can be drawn by joining them?
How many planes can be made to pass through a line and a point not on the line?
The number of dimensions, a solid has ______.
The side faces of a pyramid are ______.
Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.
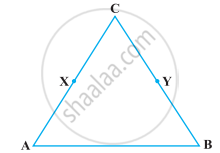
Read the following statements which are taken as axioms:
- If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
- If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent? Justify your answer.
