Advertisements
Advertisements
प्रश्न
D, E और F क्रमशः ΔABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। वो दिखाओ
(i) BDEF एक समांतर चतुर्भुज है।
(ii) ar (DEF) = `1/4`ar (ABC)
(iii) ar (BDEF) = `1/2`ar (ABC)
उत्तर

(i) In ΔABC,
E और F क्रमशः भुजा AC और AB के मध्य-बिंदु हैं।
इसलिए, EF || BC और EF = `1/2` BC (मध्य-बिंदु प्रमेय)
हालाँकि, BD = `1/2` BC (D, BC का मध्य-बिंदु है)
इसलिए, BD = EF and BD || EF
अत: BDEF एक समांतर चतुर्भुज है।
(ii) ऊपर प्राप्त परिणाम का उपयोग करते हुए, यह कहा जा सकता है कि चतुर्भुज BDEF, DCEF, AFDE समांतर चतुर्भुज हैं।
हम जानते हैं कि एक समांतर चतुर्भुज के विकर्ण इसे समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करते हैं।
∴ क्षेत्रफल (ΔBFD) = क्षेत्रफल (ΔDEF) (समांतर चतुर्भुज BD के लिए)
क्षेत्रफल (ΔCDE) = क्षेत्रफल (ΔDEF) (समानांतर चतुर्भुज DCEF के लिए)
क्षेत्रफल (ΔAFE) = क्षेत्रफल (ΔDEF) (समानांतर चतुर्भुज AFDE के लिए)
क्षेत्रफल (ΔAFE) = क्षेत्रफल (ΔBFD) = क्षेत्रफल (ΔCDE) = क्षेत्रफल (ΔDEF)
भी,
क्षेत्रफल (ΔAFE) + क्षेत्रफल (ΔBDF) + क्षेत्रफल (ΔCDE) + क्षेत्रफल (ΔDEF) = क्षेत्रफल (ΔABC)
क्षेत्र (ΔDEF) + क्षेत्र (ΔDEF) + क्षेत्र (ΔDEF) + क्षेत्र (ΔDEF) = क्षेत्र (ΔABC)
4 क्षेत्रफल (ΔDEF) = क्षेत्रफल (ΔABC)
क्षेत्रफल (ΔDEF) = `1/4` क्षेत्र (ΔABC)
(iii) क्षेत्रफल (समांतर चतुर्भुज BDEF) = क्षेत्रफल (ΔDEF) + क्षेत्रफल (ΔBDF)
क्षेत्रफल (समांतर चतुर्भुज BDEF)
= क्षेत्रफल (ΔDEF) + क्षेत्रफल (ΔDEF)
⇒ क्षेत्रफल (समांतर चतुर्भुज BDEF)
= 2 क्षेत्रफल (ΔDEF)
= क्षेत्रफल (समांतर चतुर्भुज BDEF)= `2xx1/4 "क्षेत्रफल"(ΔABC)`
= क्षेत्रफल (समांतर चतुर्भुज BDEF) = `1/2` क्षेत्र (ΔABC)
APPEARS IN
संबंधित प्रश्न
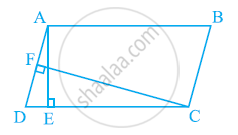
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है | यदि AB = CD है, तो दर्शाइए की
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है |
[संकेत: D और B से AC पर लंब खींचिए।]

XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
एक समलंब ABCD, जिसमें AB || DC हैं, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दर्शाइए कि ar(AOD) = ar(BOC) है |
ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
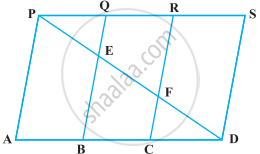
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
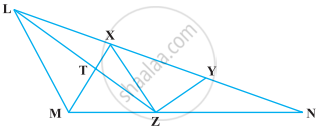
X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार हैं कि LX = XY = YN हैं। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। (देखिए आकृति)। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए :
ar (ΔABD)
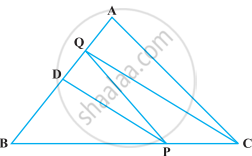
∆ABC, D भुजा AB का मध्य-बिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखंड CQ || PD भुजा AB से Q पर मिलता है (आकृति), तो सिद्ध कीजिए कि ar (BPQ) = `1/2` ar (∆ABC) है।