Advertisements
Advertisements
प्रश्न
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
उत्तर
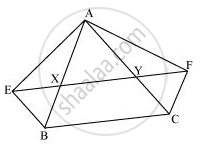
दिया जाता है कि
XY || BC ⇒ EY || BC
BE || AC ⇒ BE || CY
अत: EBCY एक समांतर चतुर्भुज है।दिया जाता है कि
XY || BC ⇒ XF || BC
FC || AB ⇒ FC || XB
अत: BCFX एक समांतर चतुर्भुज है।
समांतर चतुर्भुज EBCY और BCFX एक ही आधार BC पर और समान समांतर रेखाओं BC और EF के बीच स्थित हैं।
∴ क्षेत्रफल (EBCY) = क्षेत्रफल (BCFX) ... (1)
समांतर चतुर्भुज EBCY और AEB पर विचार करें
ये एक ही आधार BE पर स्थित हैं और एक ही समान्तर रेखाओं BE और AC के बीच स्थित हैं।
∴ क्षेत्रफल (ΔABE) = 1/2 क्षेत्रफल (EBCY) ... (2)
साथ ही, समांतर चतुर्भुज BCFX और ΔACF एक ही आधार CF पर और समान समांतर रेखाओं CF और AB के बीच स्थित हैं।
∴ क्षेत्रफल (ΔACF) = 1/2 क्षेत्रफल (BCFX) ... (3)
समीकरण (1), (2), और (3) से, हम प्राप्त करते हैं
क्षेत्रफल (ΔABE) = क्षेत्रफल (ΔACF)
APPEARS IN
संबंधित प्रश्न
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है | यदि AB = CD है, तो दर्शाइए की
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है |
[संकेत: D और B से AC पर लंब खींचिए।]

ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
निम्नलिखित आकृतियों में से किसमें आप एक ही आधार पर और एक ही समांतर रेखाओं के बीच, बने दो बहुभुज प्राप्त करते हैं :
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिंदुओं को मिलाने से बनी आकृति है :
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD ______।
PQRS एक आयत है, जो त्रिज्या 13 cm वाले एक वृत्त के चतुर्थांश के अंतर्गत है। A भुजा PQ पर स्थित कोई बिंदु है। यदि PS = 5 cm है, तो ar (PAS) = 30 cm2 है।
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। तब, ar (BDE) = `1/4` ar (ABC) है।
निम्नलिखित आकृति में, ABCD और EFGD समांतर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिंदु है। तब, ar (DPC) = `1/2` ar (EFGD) है।
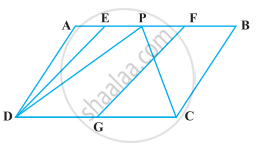
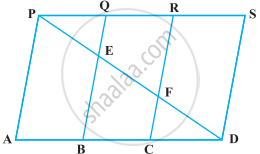
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।