Advertisements
Advertisements
प्रश्न
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिंदुओं को मिलाने से बनी आकृति है :
विकल्प
24 cm2 क्षेत्रफल का एक आयत
25 cm2 क्षेत्रफल का एक वर्ग
24 cm2 क्षेत्रफल का एक समलंब
24 cm2 क्षेत्रफल का एक समचतुर्भुज
उत्तर
24 cm2 क्षेत्रफल का एक समचतुर्भुज
स्पष्टीकरण -
दिया गया है - आयत जिसकी भुजाएँ 8 सेमी और 6 सेमी हैं।
ज्ञात करना है - आयत की संलग्न भुजाओं के मध्य बिन्दुओं को मिलाने से बनी आकृति का क्षेत्रफल।
गणना - चूँकि हम जानते हैं कि समचतुर्भुज का क्षेत्रफल = `1/2 (d_1 xx d_2)`
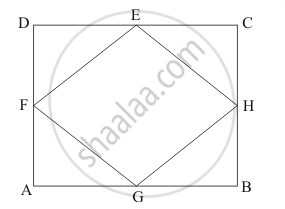
समचतुर्भुज EFGH के लिए, EG एक विकर्ण है जो DA के बराबर है।
FH दूसरा विकर्ण है जो AB के बराबर है।
समचतुर्भुज का क्षेत्रफल = `1/2 (d_1 xx d_2)`
समचतुर्भुज का क्षेत्रफल = `1/2 (8 xx 6)`
समचतुर्भुज का क्षेत्रफल = `1/2 (48)`
समचतुर्भुज का क्षेत्रफल = 24 cm2
APPEARS IN
संबंधित प्रश्न
यदि E, F, G और H क्रमशः एक समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = `1/2`ar (ABCD) हैं
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है | यदि AB = CD है, तो दर्शाइए की
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है |
[संकेत: D और B से AC पर लंब खींचिए।]

ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप इस प्रश्न का उत्तर दे सकते हैं कि आपने इस अध्याय के 'परिचय' में छोड़ दिया है कि "क्या बुधिया के खेत को वास्तव में बराबर क्षेत्रफल के तीन भागों में बांटा गया है"?
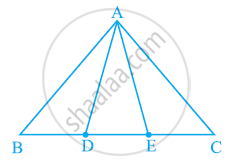
[टिप्पणी: ध्यान दें कि BD = DE = EC लेने पर त्रिभुज ABC को बराबर क्षेत्रफलों वाले तीन त्रिभुज ABD, ADE और AEC में विभाजित किया जाता है। इसी तरह, BC को n समान भागों में विभाजित करके और इस प्रकार प्राप्त विभाजन बिंदुओं को BC के विपरीत शीर्ष से जोड़कर, आप ΔABC को समान क्षेत्रफल वाले n त्रिभुजों में विभाजित कर सकते हैं।]
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल है :
एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समांतर रेखाओं के बीच स्थित हैं, तो त्रिभुज के क्षेत्रफल का समांतर चतुर्भुज के क्षेत्रफल से अनुपात है
PQRS एक आयत है, जो त्रिज्या 13 cm वाले एक वृत्त के चतुर्थांश के अंतर्गत है। A भुजा PQ पर स्थित कोई बिंदु है। यदि PS = 5 cm है, तो ar (PAS) = 30 cm2 है।
निम्नलिखित आकृति में, ABCD और EFGD समांतर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिंदु है। तब, ar (DPC) = `1/2` ar (EFGD) है।
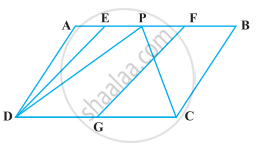
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
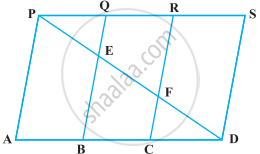
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है (आकृति)। ज्ञात कीजिए :
- ar (ABEF)
- ar (ABD)
- ar (BEF)