Advertisements
Advertisements
प्रश्न
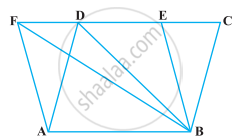
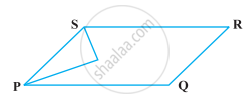
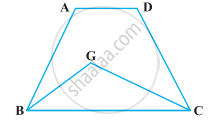
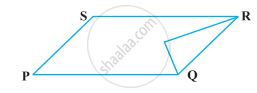
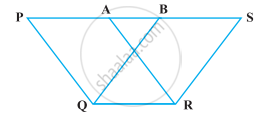
निम्नलिखित आकृतियों में से किसमें आप एक ही आधार पर और एक ही समांतर रेखाओं के बीच, बने दो बहुभुज प्राप्त करते हैं :
विकल्प
उत्तर
स्पष्टीकरण -
आकृतियों (a), (b) और (c) में एक ही आधार पर दो बहुभुज हैं लेकिन वे एक ही समांतर रेखाओं के बीच नहीं हैं।
आकृति (d) में, एक ही आधार पर और समान समांतर रेखाओं के बीच दो बहुभुज (PQRA और BQRS) हैं।
APPEARS IN
संबंधित प्रश्न
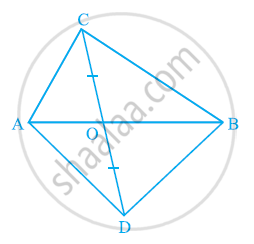
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
एक समलंब ABCD, जिसमें AB || DC हैं, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दर्शाइए कि ar(AOD) = ar(BOC) है |
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल है :
PQRS एक आयत है, जो त्रिज्या 13 cm वाले एक वृत्त के चतुर्थांश के अंतर्गत है। A भुजा PQ पर स्थित कोई बिंदु है। यदि PS = 5 cm है, तो ar (PAS) = 30 cm2 है।
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। तब, ar (BDE) = `1/4` ar (ABC) है।
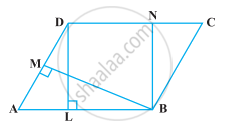
निम्नलिखित आकृति में, ABCD और EFGD समांतर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिंदु है। तब, ar (DPC) = `1/2` ar (EFGD) है।
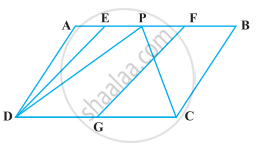
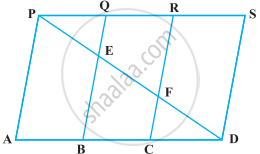
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
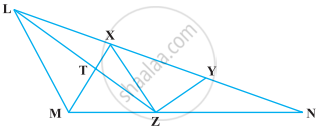
X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार हैं कि LX = XY = YN हैं। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। (देखिए आकृति)। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए :
ar (ΔABD)