Advertisements
Advertisements
प्रश्न
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप इस प्रश्न का उत्तर दे सकते हैं कि आपने इस अध्याय के 'परिचय' में छोड़ दिया है कि "क्या बुधिया के खेत को वास्तव में बराबर क्षेत्रफल के तीन भागों में बांटा गया है"?
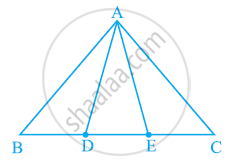
[टिप्पणी: ध्यान दें कि BD = DE = EC लेने पर त्रिभुज ABC को बराबर क्षेत्रफलों वाले तीन त्रिभुज ABD, ADE और AEC में विभाजित किया जाता है। इसी तरह, BC को n समान भागों में विभाजित करके और इस प्रकार प्राप्त विभाजन बिंदुओं को BC के विपरीत शीर्ष से जोड़कर, आप ΔABC को समान क्षेत्रफल वाले n त्रिभुजों में विभाजित कर सकते हैं।]
उत्तर
माना एक रेखाखंड खींचते हैं
AM ⊥ BC.
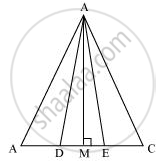
हम जानते हैं कि,
त्रिभुज का क्षेत्रफल = 1/2 × आधार × ऊँचाई
`"क्षेत्र "(triangleADE)=1/2xxDExxAM`
`"क्षेत्र"("त्रिकोणABD")=1/2xxBDxxAM`
`"क्षेत्र"("त्रिकोणAEC")=1/2xxECxxAM`
यह दिया गया है कि DE = BD = EC
`⇒ 1/2xxDExxAM=1/2xxBDxxAM=1/2xxECxxAM`
क्षेत्रफल (ΔADE) = क्षेत्रफल (ΔABD) = क्षेत्रफल (ΔAEC)
यह देखा जा सकता है कि बुधिया ने अपने खेत को 3 बराबर भागों में बांटा है।
APPEARS IN
संबंधित प्रश्न
यदि E, F, G और H क्रमशः एक समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = `1/2`ar (ABCD) हैं
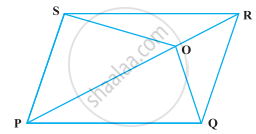
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
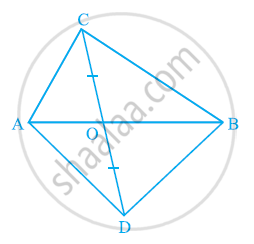
एक समलंब ABCD, जिसमें AB || DC हैं, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दर्शाइए कि ar(AOD) = ar(BOC) है |
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिंदुओं को मिलाने से बनी आकृति है :
एक त्रिभुज की भुजाओं के मध्य-बिंदु किसी भी एक शीर्ष को चौथा बिंदु लेकर एक समांतर चतुर्भुज बनाते हैं, जिसका क्षेत्रफल बराबर है
एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समांतर रेखाओं के बीच स्थित हैं, तो त्रिभुज के क्षेत्रफल का समांतर चतुर्भुज के क्षेत्रफल से अनुपात है
ABCD एक समलंब है जिसकी समांतर भुजाएँ AB = a cm और DC = b cm है (आकृति)। E और F असमांतर भुजाओं के मध्य-बिंदु हैं। ar (ABFE) और ar (EFCD) का अनुपात हैं
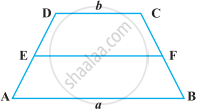
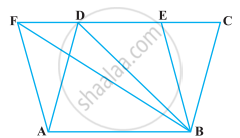
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है (आकृति)। ज्ञात कीजिए :
- ar (ABEF)
- ar (ABD)
- ar (BEF)
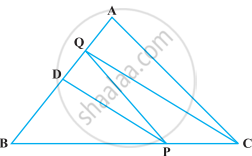
∆ABC, D भुजा AB का मध्य-बिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखंड CQ || PD भुजा AB से Q पर मिलता है (आकृति), तो सिद्ध कीजिए कि ar (BPQ) = `1/2` ar (∆ABC) है।
O एक समांतर चतुर्भुज PQRS के विकर्ण PR पर स्थित कोई बिंदु है (आकृति)। सिद्ध कीजिए कि ar (PSO) = ar (PQO) है।