Advertisements
Advertisements
Question
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप इस प्रश्न का उत्तर दे सकते हैं कि आपने इस अध्याय के 'परिचय' में छोड़ दिया है कि "क्या बुधिया के खेत को वास्तव में बराबर क्षेत्रफल के तीन भागों में बांटा गया है"?
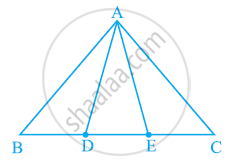
[टिप्पणी: ध्यान दें कि BD = DE = EC लेने पर त्रिभुज ABC को बराबर क्षेत्रफलों वाले तीन त्रिभुज ABD, ADE और AEC में विभाजित किया जाता है। इसी तरह, BC को n समान भागों में विभाजित करके और इस प्रकार प्राप्त विभाजन बिंदुओं को BC के विपरीत शीर्ष से जोड़कर, आप ΔABC को समान क्षेत्रफल वाले n त्रिभुजों में विभाजित कर सकते हैं।]
Solution
माना एक रेखाखंड खींचते हैं
AM ⊥ BC.
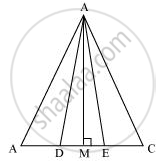
हम जानते हैं कि,
त्रिभुज का क्षेत्रफल = 1/2 × आधार × ऊँचाई
`"क्षेत्र "(triangleADE)=1/2xxDExxAM`
`"क्षेत्र"("त्रिकोणABD")=1/2xxBDxxAM`
`"क्षेत्र"("त्रिकोणAEC")=1/2xxECxxAM`
यह दिया गया है कि DE = BD = EC
`⇒ 1/2xxDExxAM=1/2xxBDxxAM=1/2xxECxxAM`
क्षेत्रफल (ΔADE) = क्षेत्रफल (ΔABD) = क्षेत्रफल (ΔAEC)
यह देखा जा सकता है कि बुधिया ने अपने खेत को 3 बराबर भागों में बांटा है।
APPEARS IN
RELATED QUESTIONS
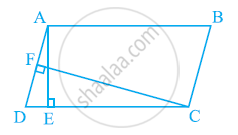
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
निम्नलिखित आकृतियों में से किसमें आप एक ही आधार पर और एक ही समांतर रेखाओं के बीच, बने दो बहुभुज प्राप्त करते हैं :
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल है :
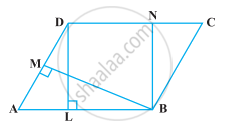
निम्नलिखित आकृति में, यदि समांतर चतुर्भुज ABCD और आयत ABEM समान क्षेत्रफल के हैं, तो ______।
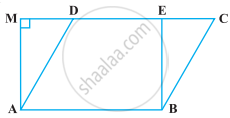
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। तब, ar (BDE) = `1/4` ar (ABC) है।
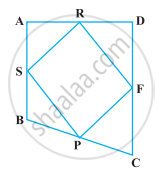
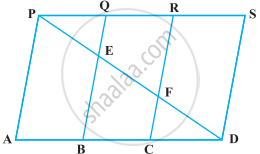
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
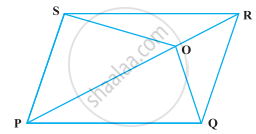
O एक समांतर चतुर्भुज PQRS के विकर्ण PR पर स्थित कोई बिंदु है (आकृति)। सिद्ध कीजिए कि ar (PSO) = ar (PQO) है।
यदि किसी चतुर्भुज की भुजाओं के मध्य-बिंदुओं को क्रम से मिलाया जाता है, तो सिद्ध कीजिए कि इस प्रकार बने समांतर चतुर्भुज का क्षेत्रफल दिए हुए चतुर्भुज के क्षेत्रफल का आधा होता है (आकृति)।
[संकेत : BD को मिलाइए और A से BD पर लंब खींचिए।]