Advertisements
Advertisements
Question
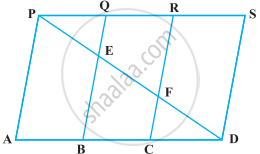
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
Solution
दिया गया है - एक समांतर चतुर्भुज PSDA में, बिंदु Q और R, PS पर इस प्रकार हैं कि
PQ = QR = RS और PA || QB || RC
सिद्ध करना है - ar (PQE) = ar (CFD)
उपपत्ति - समांतर चतुर्भुज PABQ में,
और PA || QB ...[दिया गया है।]
तो, PABQ एक समांतर चतुर्भुज है।
PQ = AB ...(i)
इसी प्रकार, QBCR भी एक समांतर चतुर्भुज है।
QR = BC ...(ii)
और RCDS एक समांतर चतुर्भुज है।
RS = CD ...(iii)
अब, PQ = QR = RS ...(iv)
समीकरण (i), (ii), (iii) और (iv) से,
PQ || AB ...[∴ समान्तर चतुर्भुज PSDA में, PS || AD]
ΔPQE और ΔDCF में,
∠QPE = ∠FDC ...[चूंकि, PS || AD और PD तिर्यक रेखा है, तो एकांतर अंत: कोण बराबर होते हैं।]
PQ = CD ...[समीकरण (v) से]
और ∠PQE = ∠FCD ...[∴ ∠PQE = ∠PRC संगत कोण और ∠PRC = ∠FCD वैकल्पिक आंतरिक कोण]
ΔPQE = ΔDCF ...[ASA सर्वांगसमता नियम द्वारा]
∴ ar (ΔPQE) = ar (ΔCFD) ...[चूँकि, सर्वांगसम आकृतियों का क्षेत्रफल समान होता है।]
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
यदि E, F, G और H क्रमशः एक समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = `1/2`ar (ABCD) हैं
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
निम्नलिखित आकृतियों में से किसमें आप एक ही आधार पर और एक ही समांतर रेखाओं के बीच, बने दो बहुभुज प्राप्त करते हैं :
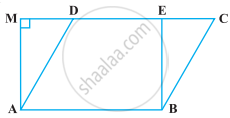
निम्नलिखित आकृति में, यदि समांतर चतुर्भुज ABCD और आयत ABEM समान क्षेत्रफल के हैं, तो ______।
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD ______।
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। तब, ar (BDE) = `1/4` ar (ABC) है।
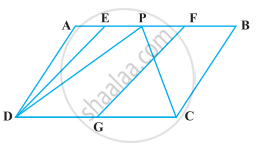
निम्नलिखित आकृति में, ABCD और EFGD समांतर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिंदु है। तब, ar (DPC) = `1/2` ar (EFGD) है।
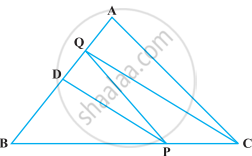
∆ABC, D भुजा AB का मध्य-बिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखंड CQ || PD भुजा AB से Q पर मिलता है (आकृति), तो सिद्ध कीजिए कि ar (BPQ) = `1/2` ar (∆ABC) है।