Advertisements
Advertisements
Question
यदि E, F, G और H क्रमशः एक समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = `1/2`ar (ABCD) हैं
Solution
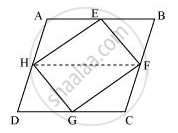
HF से जुड़ें।
समांतर चतुर्भुज ABCD में,
AD = BC और एडी || BC (एक समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर और समानांतर होती हैं)
AB = CD (एक समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं)
`1/2` AD = `1/2` BC और AH || BF के
AH = BF और AH || BF (∵ H और F AD और BC के मध्य-बिंदु हैं)
अत: ABFH एक समांतर चतुर्भुज है।
चूँकि HEF और समांतर चतुर्भुज ABFH एक ही आधार HF और समान समानांतर रेखाओं AB और HF के बीच स्थित हैं,
क्षेत्रफल (ΔHEF) = `1/2` क्षेत्र (ABFH) ... (1)
इसी प्रकार, यह सिद्ध किया जा सकता है कि
क्षेत्रफल (ΔHGF) = 1/2क्षेत्र (HDCF) ... (2)
समीकरण (1) और (2) को जोड़ने पर, हम प्राप्त करते हैं
क्षेत्र(ΔHEF) + क्षेत्र (ΔHGF) = `1/2` क्षेत्र (ABFH) + `1/2` क्षेत्र (HDCF)
= `1/2` [क्षेत्रफल (ABFH) + क्षेत्रफल (HDCF)]
क्षेत्रफल (EFGH) = `1/2` क्षेत्र (ABCD)
APPEARS IN
RELATED QUESTIONS
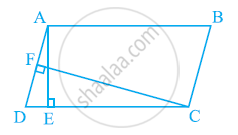
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
D, E और F क्रमशः ΔABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। वो दिखाओ
(i) BDEF एक समांतर चतुर्भुज है।
(ii) ar (DEF) = `1/4`ar (ABC)
(iii) ar (BDEF) = `1/2`ar (ABC)
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
एक त्रिभुज की भुजाओं के मध्य-बिंदु किसी भी एक शीर्ष को चौथा बिंदु लेकर एक समांतर चतुर्भुज बनाते हैं, जिसका क्षेत्रफल बराबर है
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
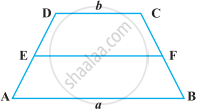
ABCD एक समलंब है जिसकी समांतर भुजाएँ AB = a cm और DC = b cm है (आकृति)। E और F असमांतर भुजाओं के मध्य-बिंदु हैं। ar (ABFE) और ar (EFCD) का अनुपात हैं
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
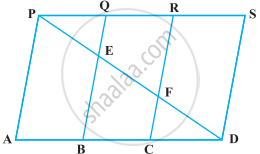
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है (आकृति)। ज्ञात कीजिए :
- ar (ABEF)
- ar (ABD)
- ar (BEF)
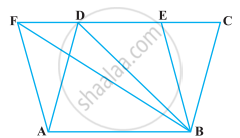
एक समलंब ABCD में, AB || DC है तथा L भुजा BC का मध्य-बिंदु है। L से होकर, एक रेखा PQ || AD खींची गई है, जो AB को P पर और बढ़ाई गई DC को Q पर मिलती है (आकृति), सिद्ध कीजिए ar (ABCD) = ar (APQD)
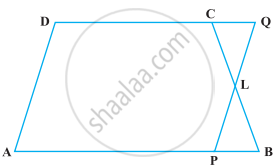
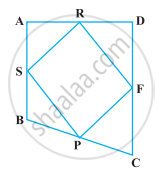
यदि किसी चतुर्भुज की भुजाओं के मध्य-बिंदुओं को क्रम से मिलाया जाता है, तो सिद्ध कीजिए कि इस प्रकार बने समांतर चतुर्भुज का क्षेत्रफल दिए हुए चतुर्भुज के क्षेत्रफल का आधा होता है (आकृति)।
[संकेत : BD को मिलाइए और A से BD पर लंब खींचिए।]