Advertisements
Advertisements
Question
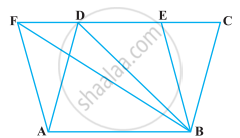
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है (आकृति)। ज्ञात कीजिए :
- ar (ABEF)
- ar (ABD)
- ar (BEF)
Solution
दिया गया है, समांतर चतुर्भुज का क्षेत्रफल, ABCD = 90 cm2
i. हम जानते हैं कि, समान आधार और समान समांतर रेखाओं के बीच बने समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
यहाँ, समान्तर चतुर्भुज ABCD और ABEF एक ही आधार AB पर और एक ही समांतर रेखाओं AB और CF के बीच हैं।
तो, ar (ΔBEF) = ar (ABCD) = 90 सेमी2
ii. हम जानते हैं कि, यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समांतर रेखाओं के बीच हों, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल के आधे के बराबर होता है।
यहाँ, ΔABD और समांतर चतुर्भुज ABCD एक ही आधार AB पर और एक ही समांतर रेखाओं AB और CD के बीच हैं।
तो, ar (ΔABD) = `1/2` ar (ABCD)
= `1/2 xx 90` ...[∴ ar (ABCD) = 90 सेमी2]
= 45 सेमी2
iii. यहाँ, ABEF और समांतर चतुर्भुज ABEF एक ही आधार EF पर और एक ही समांतर रेखाओं AB और EF के बीच हैं।
ar (ΔBEF) = `1/2` ar (ABEF)
= `1/2 xx 90` ...[∴ ar (ABEF) = 90 cm2, भाग (i) से]
= 45 cm2
APPEARS IN
RELATED QUESTIONS
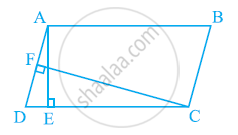
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
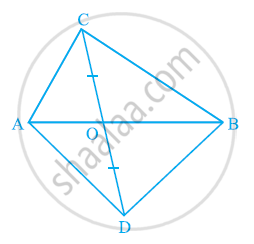
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD ______।
एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समांतर रेखाओं के बीच स्थित हैं, तो त्रिभुज के क्षेत्रफल का समांतर चतुर्भुज के क्षेत्रफल से अनुपात है
PQRS एक आयत है, जो त्रिज्या 13 cm वाले एक वृत्त के चतुर्थांश के अंतर्गत है। A भुजा PQ पर स्थित कोई बिंदु है। यदि PS = 5 cm है, तो ar (PAS) = 30 cm2 है।
निम्नलिखित आकृति में, ABCD और EFGD समांतर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिंदु है। तब, ar (DPC) = `1/2` ar (EFGD) है।
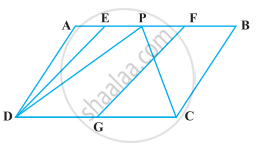
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
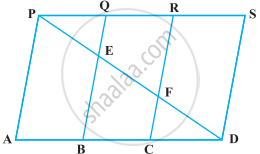
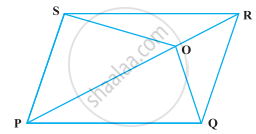
O एक समांतर चतुर्भुज PQRS के विकर्ण PR पर स्थित कोई बिंदु है (आकृति)। सिद्ध कीजिए कि ar (PSO) = ar (PQO) है।