Advertisements
Advertisements
Question
D, E और F क्रमशः ΔABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। वो दिखाओ
(i) BDEF एक समांतर चतुर्भुज है।
(ii) ar (DEF) = `1/4`ar (ABC)
(iii) ar (BDEF) = `1/2`ar (ABC)
Solution

(i) In ΔABC,
E और F क्रमशः भुजा AC और AB के मध्य-बिंदु हैं।
इसलिए, EF || BC और EF = `1/2` BC (मध्य-बिंदु प्रमेय)
हालाँकि, BD = `1/2` BC (D, BC का मध्य-बिंदु है)
इसलिए, BD = EF and BD || EF
अत: BDEF एक समांतर चतुर्भुज है।
(ii) ऊपर प्राप्त परिणाम का उपयोग करते हुए, यह कहा जा सकता है कि चतुर्भुज BDEF, DCEF, AFDE समांतर चतुर्भुज हैं।
हम जानते हैं कि एक समांतर चतुर्भुज के विकर्ण इसे समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करते हैं।
∴ क्षेत्रफल (ΔBFD) = क्षेत्रफल (ΔDEF) (समांतर चतुर्भुज BD के लिए)
क्षेत्रफल (ΔCDE) = क्षेत्रफल (ΔDEF) (समानांतर चतुर्भुज DCEF के लिए)
क्षेत्रफल (ΔAFE) = क्षेत्रफल (ΔDEF) (समानांतर चतुर्भुज AFDE के लिए)
क्षेत्रफल (ΔAFE) = क्षेत्रफल (ΔBFD) = क्षेत्रफल (ΔCDE) = क्षेत्रफल (ΔDEF)
भी,
क्षेत्रफल (ΔAFE) + क्षेत्रफल (ΔBDF) + क्षेत्रफल (ΔCDE) + क्षेत्रफल (ΔDEF) = क्षेत्रफल (ΔABC)
क्षेत्र (ΔDEF) + क्षेत्र (ΔDEF) + क्षेत्र (ΔDEF) + क्षेत्र (ΔDEF) = क्षेत्र (ΔABC)
4 क्षेत्रफल (ΔDEF) = क्षेत्रफल (ΔABC)
क्षेत्रफल (ΔDEF) = `1/4` क्षेत्र (ΔABC)
(iii) क्षेत्रफल (समांतर चतुर्भुज BDEF) = क्षेत्रफल (ΔDEF) + क्षेत्रफल (ΔBDF)
क्षेत्रफल (समांतर चतुर्भुज BDEF)
= क्षेत्रफल (ΔDEF) + क्षेत्रफल (ΔDEF)
⇒ क्षेत्रफल (समांतर चतुर्भुज BDEF)
= 2 क्षेत्रफल (ΔDEF)
= क्षेत्रफल (समांतर चतुर्भुज BDEF)= `2xx1/4 "क्षेत्रफल"(ΔABC)`
= क्षेत्रफल (समांतर चतुर्भुज BDEF) = `1/2` क्षेत्र (ΔABC)
APPEARS IN
RELATED QUESTIONS
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
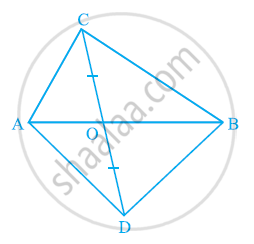
एक समलंब ABCD, जिसमें AB || DC हैं, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दर्शाइए कि ar(AOD) = ar(BOC) है |
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप इस प्रश्न का उत्तर दे सकते हैं कि आपने इस अध्याय के 'परिचय' में छोड़ दिया है कि "क्या बुधिया के खेत को वास्तव में बराबर क्षेत्रफल के तीन भागों में बांटा गया है"?
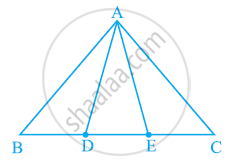
[टिप्पणी: ध्यान दें कि BD = DE = EC लेने पर त्रिभुज ABC को बराबर क्षेत्रफलों वाले तीन त्रिभुज ABD, ADE और AEC में विभाजित किया जाता है। इसी तरह, BC को n समान भागों में विभाजित करके और इस प्रकार प्राप्त विभाजन बिंदुओं को BC के विपरीत शीर्ष से जोड़कर, आप ΔABC को समान क्षेत्रफल वाले n त्रिभुजों में विभाजित कर सकते हैं।]
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिंदुओं को मिलाने से बनी आकृति है :
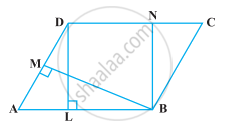
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल है :
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD ______।
एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समांतर रेखाओं के बीच स्थित हैं, तो त्रिभुज के क्षेत्रफल का समांतर चतुर्भुज के क्षेत्रफल से अनुपात है
PQRS एक आयत है, जो त्रिज्या 13 cm वाले एक वृत्त के चतुर्थांश के अंतर्गत है। A भुजा PQ पर स्थित कोई बिंदु है। यदि PS = 5 cm है, तो ar (PAS) = 30 cm2 है।
निम्नलिखित आकृति में, ABCD और EFGD समांतर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिंदु है। तब, ar (DPC) = `1/2` ar (EFGD) है।
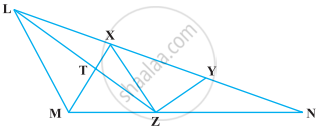
X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार हैं कि LX = XY = YN हैं। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। (देखिए आकृति)। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।