Advertisements
Advertisements
Question
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है | यदि AB = CD है, तो दर्शाइए की
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है |
[संकेत: D और B से AC पर लंब खींचिए।]

Solution
ΔDOC तथा ΔAOB में
CD = AB (दिया है)
OD = OB (दिया है)
∠COD = ∠AOB (शीर्षाभिमुख कोण)
इसलिए, SAS सर्वांगसमता नियम से
ΔDOC ≅ ΔAOB
∠DCO = ∠BAO ...... (i) BY CPCT
चूँकि ΔDOC ≅ ΔAOB इसलिए
ar (DOC) = ar (AOB) ....(ii)
(सर्वांगसम त्रिभुज क्षेत्रफल में बराबर होते है )
समी० (ii) दोनों तरफ ar(BOC) जोड़ने पर
ar (DOC) + ar(BOC) = ar (AOB) + ar(BOC)
या ar(DCB) = ar (ACB)
समी० (i) से
∠DCO = ∠BAO ...... (एकांतर कोण)
इसलिए, CD || AB और CD = AB दिया है |
अत: ABCD एक समांतर चतुर्भुज है |
(सम्मुख भुजाओं के एक युग्म बराबर और समांतर हो तो वह समांतर चतुर्भुज होता है)
इसलिए DA || CB या ABCD एक समांतर चतुर्भुज है
APPEARS IN
RELATED QUESTIONS
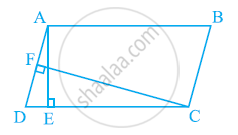
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
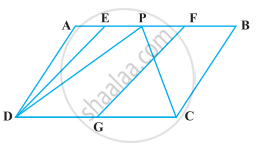
यदि E, F, G और H क्रमशः एक समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = `1/2`ar (ABCD) हैं
एक समलंब ABCD, जिसमें AB || DC हैं, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दर्शाइए कि ar(AOD) = ar(BOC) है |
ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिंदुओं को मिलाने से बनी आकृति है :
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
PQRS एक आयत है, जो त्रिज्या 13 cm वाले एक वृत्त के चतुर्थांश के अंतर्गत है। A भुजा PQ पर स्थित कोई बिंदु है। यदि PS = 5 cm है, तो ar (PAS) = 30 cm2 है।
निम्नलिखित आकृति में, ABCD और EFGD समांतर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिंदु है। तब, ar (DPC) = `1/2` ar (EFGD) है।
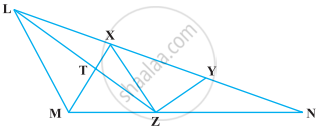
X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार हैं कि LX = XY = YN हैं। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। (देखिए आकृति)। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।
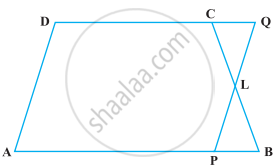
एक समलंब ABCD में, AB || DC है तथा L भुजा BC का मध्य-बिंदु है। L से होकर, एक रेखा PQ || AD खींची गई है, जो AB को P पर और बढ़ाई गई DC को Q पर मिलती है (आकृति), सिद्ध कीजिए ar (ABCD) = ar (APQD)