Advertisements
Advertisements
Question
बिंदु D और E क्रमश: ΔABC कि भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC) = ar(EBC) है दर्शाइए कि DE || BC है |
Solution
दिया है: बिंदु D और E क्रमश: DABC कि भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC) = ar(EBC) है |
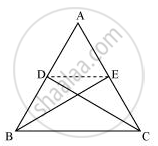
सिद्ध करना है:
DE || BC
प्रमाण:
ΔDBC और ΔEBC एक ही आधार BC और क्षेत्रफल में बराबर है क्योंकि
ar(DBC) = ar(EBC) दिया है |
अत: प्रमेय 9.3 से
DE || BC
APPEARS IN
RELATED QUESTIONS
एक त्रिभुज ΔABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = `1/4`ar (ABC) है।
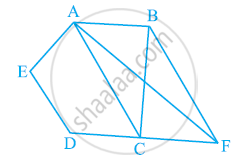
ABCDE एक पंचभुज है| B से होकर AC के समांतर खिंची गई रेखा बढाई गई DC को F पर मिलती है | दर्शाइए कि
(i) ar(ACB) = ar(ACF)
(ii) ar(AEDF) = ar(ABCDE)
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध् के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है सिद्ध कीजिए कि ABCD एक समलंब है |
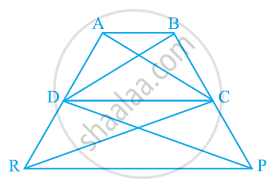
दी गई आकृति में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है | दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब है |
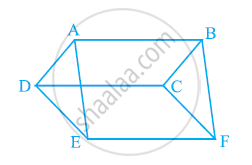
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर काटते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लंब खींचिए।]
किसी समांतर चतुर्भुज ABCD की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती हैं। सिद्ध कीजिए कि ar (ADF) = ar (ABFC) है।
एक समांतर चतुर्भुज ABCD के विकर्ण बिंदु O पर प्रतिच्छेद करते हैं। O से होकर एक रेखा खींची जाती है, जो AD को P और BC से Q पर मिलती है। दर्शाइए कि PQ इस समांतर चतुर्भुज ABCD को बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है।
त्रिभुज ABC में यदि L और M क्रमश : AB और AC भुजाओं पर इस प्रकार स्थित बिंदु हैं कि LM || BC है। सिद्ध कीजिए कि ar (LOB) = ar (MOC) है।
