Advertisements
Advertisements
Question
एक समांतर चतुर्भुज ABCD के विकर्ण बिंदु O पर प्रतिच्छेद करते हैं। O से होकर एक रेखा खींची जाती है, जो AD को P और BC से Q पर मिलती है। दर्शाइए कि PQ इस समांतर चतुर्भुज ABCD को बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है।
Solution
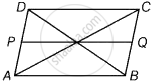
दिया गया है - एक समांतर चतुर्भुज ABCD में, विकर्ण O पर प्रतिच्छेद करते हैं और एक रेखा PQ खींचते हैं, जो AD और BC को प्रतिच्छेद करती है।
सिद्ध करना है - PQ समांतर चतुर्भुज ABCD को समान क्षेत्रफल वाले दो भागों में विभाजित करता है।
अर्थात्, ar (ABQP) = ar (CDPQ)
उपपत्ति - हम जानते हैं कि, समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।
∴ OA = OC और OB = OD ...(i)
ΔAOB और ΔCOD में,
OA = OC
OB = OD ...[समीकरण (i) से]
और ∠AOB = ∠COD ...[शीर्षाभिमुख कोण]
∴ ΔAOB = ΔCOD ...[SAS सर्वांगसमता नियम द्वारा]
तब, ar (ΔAOB) = ar (ΔCOD) ...(ii) [चूँकि सर्वांगसम आकृतियों का क्षेत्रफल समान होता है।]
अब, ΔAOP और ΔCOQ में,
∠PAO = ∠OCQ ...[वैकल्पिक आंतरिक कोण]
OA = OC ...[समीकरण (i) से]
और ∠AOP = ∠COQ ...[शीर्षाभिमुख कोण]
∴ ΔAOP ≅ ΔCOQ ...[ASA सर्वांगसमता नियम द्वारा]
∴ ar (ΔAOP) = ar (ΔCOQ) ...(iii) [चूँकि, सर्वांगसम आकृतियों का क्षेत्रफल बराबर होता है।]
इसी प्रकार, ar (ΔPOD) = ar (ΔBOQ) ...(iv)
अब, ar (ABQP) = ar (ΔCOQ) + ar (ΔCOD) + ar (ΔPOD)
= ar (ΔAOP) + ar (ΔAOB) + ar (ΔBOQ) ...[समीकरण (ii), (iii) और (iv) से]
⇒ ar (ABQP) = ar (CDPQ)
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
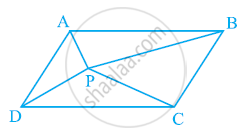
दी गई आकृति में, P एक समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। वो दिखाओ
(i) ar (APB) + ar (PCD) = `1/2`ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[संकेत: के माध्यम से। P, AB के समांतर एक रेखा खींचिए]
एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। क्षेत्र को कितने भागों में विभाजित किया गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए?
दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढाया गया है | A से होकर CP के समांतर खिंची गई रेखा बढाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है | दर्शाइए कि ar(ABCD) = ar(PBQR) है |
[संकेत: AC और PQ को मिलाइए अब ar(ACQ) और ar(APQ) कि तुलना कीजिये]
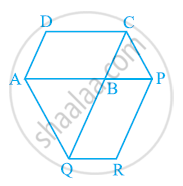
दी गई आकृति में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है | दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब है |
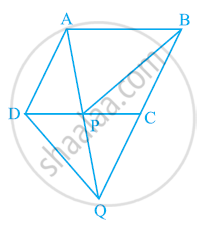
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ)
[संकेत AC को मिलाइए।]
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D, भुजा BC का मध्य-बिंदु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
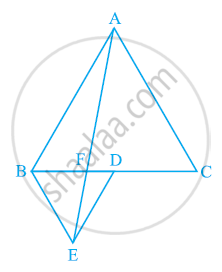
(i) ar (BDE) = `1/4` ar (ABC)
(ii) ar (BDE) = `1/2` ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = `1/8`ar (AFC)
[संकेत : EC और AD को मिलाइए। दिखाओ कि BE || AC and DE || AB, आदि]
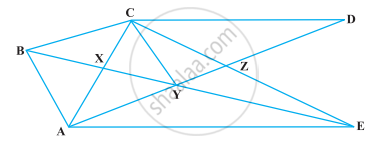
निम्नलिखित आकृति में, CD || AE और CY || BA है। सिद्ध कीजिए कि ar (CBX) = ar (AXY) है।
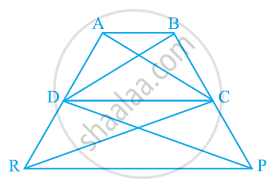
ABCD एक समलंब है, जिसमें AB || DC, DC = 30 cm और AB = 50 cm है। यदि X और Y क्रमश : AD और BC के मध्य-बिंदु हैं, तो सिद्ध कीजिए कि ar (DCYX) = `7/9` ar (XYBA) है।
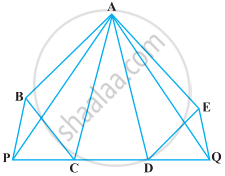
निम्नलिखित आकृति में, ABCDE एक पंचभुज है। AC के समांतर खींची गई BP बढ़ाई गई DC को P पर तथा AD के समांतर खींची गई EQ बढ़ाई गई CD से Q पर मिलती है। सिद्ध कीजिए कि ar (ABCDE) = ar (APQ) है।