Advertisements
Advertisements
Question
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D, भुजा BC का मध्य-बिंदु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
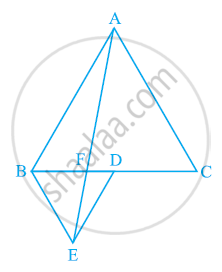
(i) ar (BDE) = `1/4` ar (ABC)
(ii) ar (BDE) = `1/2` ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = `1/8`ar (AFC)
[संकेत : EC और AD को मिलाइए। दिखाओ कि BE || AC and DE || AB, आदि]
Solution
(i) माना G और H क्रमशः भुजा AB और AC के मध्य-बिंदु हैं।
रेखा खंड GH मध्य-बिंदुओं को मिला रहा है। इसलिए, यह तीसरी भुजा BC के समानांतर होगा और इसकी लंबाई भी BC (मध्य-बिंदु प्रमेय) की लंबाई की आधी होगी।
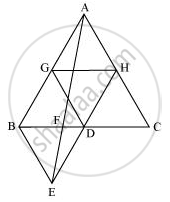
⇒ GH = 1/2BC और GH || BD
⇒ GH = BD = DC और GH || BD (D, का मध्य-बिंदु है BC)
चतुर्भुज पर विचार करें GHDB
GH ||BD और GH = BD
समान लंबाई के दो समानांतर रेखाखंडों को मिलाने वाले दो रेखाखंड भी बराबर और एक दूसरे के समानांतर होंगे।
इसलिए, BG = DH and BG || DH
अत: चतुर्भुज GHDB एक समांतर चतुर्भुज है।
हम जानते हैं कि एक समांतर चतुर्भुज में विकर्ण उसे समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है।
अत: क्षेत्रफल (ΔBDG) = क्षेत्रफल (ΔHGD)
इसी प्रकार, यह सिद्ध किया जा सकता है कि चतुर्भुज DCHG, GDHA और BEDG समांतर चतुर्भुज हैं और उनके संबंधित विकर्ण उन्हें समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित कर रहे हैं।
ar (ΔGDH) = ar (ΔCHD) (समानांतर चतुर्भुज के लिए DCHG)
ar (ΔGDH) = ar (ΔHAG) (समानांतर चतुर्भुज के लिए GDHA)
ar (ΔBDE) = ar (ΔDBG) समानांतर चतुर्भुज BEEG के लिए)
ar (ΔABC) = ar(ΔBDG) + ar(ΔGDH) + ar(ΔDCH) + ar(ΔAGH)
ar (ΔABC) = 4 × ar(ΔBDE)
Hence, ar(BDE) = 1/4 ar(ABC)
(ii) क्षेत्रफल (ΔBDE) = क्षेत्रफल (ΔAED) (सामान्य आधार DE और DE||AB)
क्षेत्र (ΔADE) - क्षेत्र (ΔFED) = क्षेत्र (ΔADE) - क्षेत्र (ΔFED) क्षेत्रफल (ΔDEF) = क्षेत्रफल (ΔAFD) (1) क्षेत्रफल (ΔABD) = क्षेत्रफल (ΔABF) + क्षेत्रफल (ΔAFD)
क्षेत्रफल (ΔABD) = क्षेत्रफल (ΔABE) (2)
AD में माध्यिका है। ΔABC.
`ar(ΔABD) = 1/2 ar(ΔABC)`
`= 1/4ar(ΔBDE)" (जैसा कि पहले साबित हुआ)"`
`ar(ΔABD) = 2ar(ΔBDE)" ........(3)"`
(2) और (3) से, हम प्राप्त करते हैं
2 ar (ΔBDE) = ar (ΔABE)
और, ar(ΔBDE) = 1/2ar(ΔABE)
(iii)
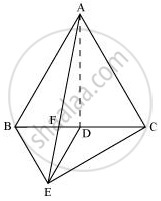
ar (ΔABE) = ar (ΔBEC) (सामान्य आधार BE और BE||AC)
ar (ΔABF) + ar (ΔBEF) = ar (ΔBEC)
समीकरण (1) का उपयोग करके, हम प्राप्त करते हैं
ar (ΔABF) + ar (ΔAFD) = ar (ΔBEC)
ar (ΔABD) = ar (ΔBEC)
1/2 ar(ΔABC) = ar(ΔBEC)
ar (ΔABC) = 2 ar (ΔBEC)
(iv) यह देखा गया है कि ΔBDE और ar ΔAED एक ही आधार (DE) पर और समानांतर DE और AB के बीच स्थित हैं।
∴ ar (ΔBDE) = ar (ΔAED)
⇒ ar (ΔBDE) − ar (ΔFED) = ar (ΔAED) − ar (ΔFED)
∴ ar (ΔBFE) = ar (ΔAFD)
(v) मान लीजिए कि शीर्ष E की ऊंचाई h है, जो BDE में भुजा BD के संगत है।
मान लीजिए कि H शीर्ष ए की ऊंचाई है, जो कि BC की भुजा के अनुरूप है
ΔABC.
(i) में, यह दिखाया गया था कि ar (BDE) = 1/4ar(ABC).
`therefore1/2xxBDxxh=1/4(1/2xxBCxxH)`
`rArrBDxxh=1/4(2BDxxH)`
`rArrh=1/2H`
(iv) में, यह दिखाया गया था कि ar
(ΔBFE) = ar (ΔAFD).
∴ ar (ΔBFE) = ar (ΔAFD)
`=1/2xxFDxxH=1/2xxFDxx2h=2(1/2xxFDxxh)`
= 2 ar (ΔFED)
`"इसलिये, "ar(BFE) = 2ar(FED)`
(iv) क्षेत्र (AFC) = क्षेत्र (AFD) + क्षेत्र (ADC)
`=ar(BFE)+1/2ar(ABC)" "["In (v), "ar(BFE) = ar(AFD);" AD is median of ΔABC"]`
`=ar(BFE)+1/2xx4ar(BDE)" "["In (i), "ar(BDE)=1/4ar(ABC)]" Now, by (v),"`
= ar(BFE) + 2ar(BDE) ............(5)
ar(BFE) = 2ar(FED) ...........(6)
ar(BDE) = ar(BFE) + ar(FED) = 2ar(FED) + ar(FED) = 3ar(FED) .........(7)
इसलिए, समीकरणों (5), (6), और (7) से, हम प्राप्त करते हैं:
ar(AFC) = 2ar(FED) + 2 x 3ar(FED) = 8ar(FED)
∴ ar(AFC) = 8ar(FED)
`"इसलिये", ar(FED) = 1/8ar(AFC)`
APPEARS IN
RELATED QUESTIONS
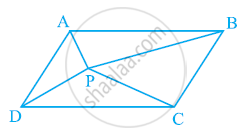
दी गई आकृति में, P एक समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। वो दिखाओ
(i) ar (APB) + ar (PCD) = `1/2`ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[संकेत: के माध्यम से। P, AB के समांतर एक रेखा खींचिए]
एक त्रिभुज ΔABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = `1/4`ar (ABC) है।
दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
बिंदु D और E क्रमश: ΔABC कि भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC) = ar(EBC) है दर्शाइए कि DE || BC है |
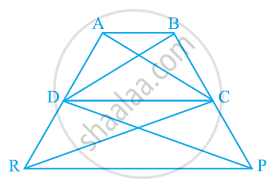
दी गई आकृति में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है | दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब है |
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
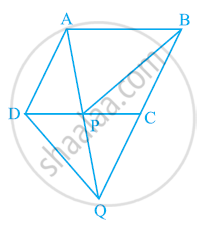
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ)
[संकेत AC को मिलाइए।]
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः BC, CA और AB भुजाओं पर वर्ग हैं। रेखा खंड AX ⊥ DE, भुजा BC से Y पर मिलता है। दर्शाइए कि:
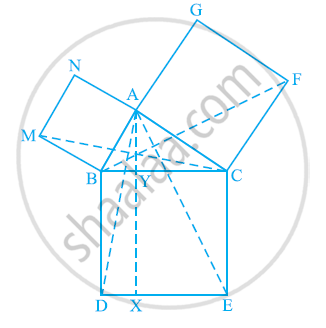
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
नोट: परिणाम (vii) पाइथागोरस का प्रसिद्ध प्रमेय है। आप कक्षा X में इस प्रमेय के सरल प्रमाण के बारे में जानेंगे।
किसी समांतर चतुर्भुज ABCD की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती हैं। सिद्ध कीजिए कि ar (ADF) = ar (ABFC) है।
एक समांतर चतुर्भुज ABCD के विकर्ण बिंदु O पर प्रतिच्छेद करते हैं। O से होकर एक रेखा खींची जाती है, जो AD को P और BC से Q पर मिलती है। दर्शाइए कि PQ इस समांतर चतुर्भुज ABCD को बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है।
