Advertisements
Advertisements
प्रश्न
एक समांतर चतुर्भुज ABCD के विकर्ण बिंदु O पर प्रतिच्छेद करते हैं। O से होकर एक रेखा खींची जाती है, जो AD को P और BC से Q पर मिलती है। दर्शाइए कि PQ इस समांतर चतुर्भुज ABCD को बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है।
उत्तर
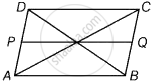
दिया गया है - एक समांतर चतुर्भुज ABCD में, विकर्ण O पर प्रतिच्छेद करते हैं और एक रेखा PQ खींचते हैं, जो AD और BC को प्रतिच्छेद करती है।
सिद्ध करना है - PQ समांतर चतुर्भुज ABCD को समान क्षेत्रफल वाले दो भागों में विभाजित करता है।
अर्थात्, ar (ABQP) = ar (CDPQ)
उपपत्ति - हम जानते हैं कि, समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।
∴ OA = OC और OB = OD ...(i)
ΔAOB और ΔCOD में,
OA = OC
OB = OD ...[समीकरण (i) से]
और ∠AOB = ∠COD ...[शीर्षाभिमुख कोण]
∴ ΔAOB = ΔCOD ...[SAS सर्वांगसमता नियम द्वारा]
तब, ar (ΔAOB) = ar (ΔCOD) ...(ii) [चूँकि सर्वांगसम आकृतियों का क्षेत्रफल समान होता है।]
अब, ΔAOP और ΔCOQ में,
∠PAO = ∠OCQ ...[वैकल्पिक आंतरिक कोण]
OA = OC ...[समीकरण (i) से]
और ∠AOP = ∠COQ ...[शीर्षाभिमुख कोण]
∴ ΔAOP ≅ ΔCOQ ...[ASA सर्वांगसमता नियम द्वारा]
∴ ar (ΔAOP) = ar (ΔCOQ) ...(iii) [चूँकि, सर्वांगसम आकृतियों का क्षेत्रफल बराबर होता है।]
इसी प्रकार, ar (ΔPOD) = ar (ΔBOQ) ...(iv)
अब, ar (ABQP) = ar (ΔCOQ) + ar (ΔCOD) + ar (ΔPOD)
= ar (ΔAOP) + ar (ΔAOB) + ar (ΔBOQ) ...[समीकरण (ii), (iii) और (iv) से]
⇒ ar (ABQP) = ar (CDPQ)
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
P और Q एक समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित कोई दो बिंदु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
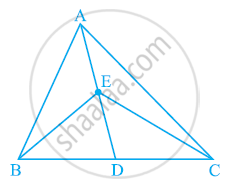
दी गई आकृति में, ΔABC की माध्यिका AD पर स्थित E कोई बिंदु है। दिखाएँ कि ar (ABE) = ar (ACE) है।
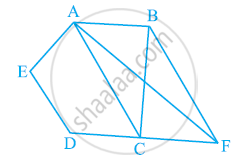
ABCDE एक पंचभुज है| B से होकर AC के समांतर खिंची गई रेखा बढाई गई DC को F पर मिलती है | दर्शाइए कि
(i) ar(ACB) = ar(ACF)
(ii) ar(AEDF) = ar(ABCDE)
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध् के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है सिद्ध कीजिए कि ABCD एक समलंब है |
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः BC, CA और AB भुजाओं पर वर्ग हैं। रेखा खंड AX ⊥ DE, भुजा BC से Y पर मिलता है। दर्शाइए कि:
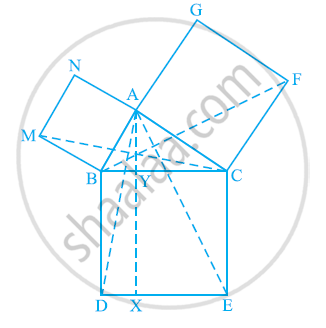
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
नोट: परिणाम (vii) पाइथागोरस का प्रसिद्ध प्रमेय है। आप कक्षा X में इस प्रमेय के सरल प्रमाण के बारे में जानेंगे।
किसी समांतर चतुर्भुज ABCD की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती हैं। सिद्ध कीजिए कि ar (ADF) = ar (ABFC) है।
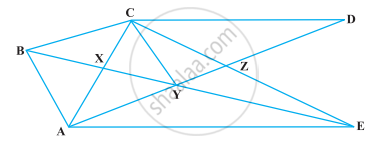
निम्नलिखित आकृति में, CD || AE और CY || BA है। सिद्ध कीजिए कि ar (CBX) = ar (AXY) है।
त्रिभुज ABC में यदि L और M क्रमश : AB और AC भुजाओं पर इस प्रकार स्थित बिंदु हैं कि LM || BC है। सिद्ध कीजिए कि ar (LOB) = ar (MOC) है।
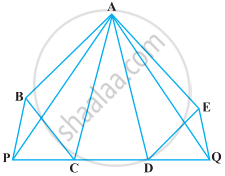
निम्नलिखित आकृति में, ABCDE एक पंचभुज है। AC के समांतर खींची गई BP बढ़ाई गई DC को P पर तथा AD के समांतर खींची गई EQ बढ़ाई गई CD से Q पर मिलती है। सिद्ध कीजिए कि ar (ABCDE) = ar (APQ) है।