Advertisements
Advertisements
प्रश्न
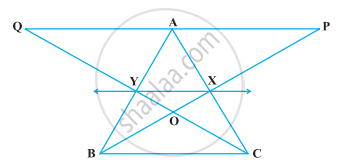
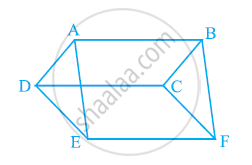
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः BC, CA और AB भुजाओं पर वर्ग हैं। रेखा खंड AX ⊥ DE, भुजा BC से Y पर मिलता है। दर्शाइए कि:
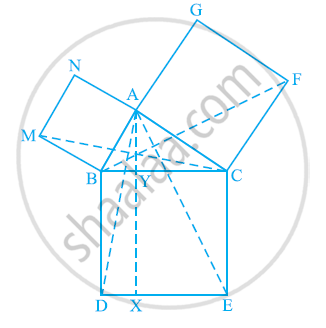
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
नोट: परिणाम (vii) पाइथागोरस का प्रसिद्ध प्रमेय है। आप कक्षा X में इस प्रमेय के सरल प्रमाण के बारे में जानेंगे।
उत्तर
(i) हम जानते हैं कि एक वर्ग का प्रत्येक कोण 90° का होता है।
इसलिये,
∠ABM = ∠DBC = 90º
⇒ ∠ABM + ∠ABC = ∠DBC + ∠ABC
⇒ ∠MBC = ∠ABD
In ΔMBC and ΔABD,
∠MBC = ∠ABD (ऊपर प्रदान किया गया)
MB = AB (वर्ग के किनारे ABMN)
BC = BD (वर्ग के किनारे BCED)
∴ ΔMBC ≅ ΔABD (SAS सर्वांगसमता नियम)
(ii) अपने पास
ΔMBC ≅ ΔABD
⇒ ar (ΔMBC) = ar (ΔABD) ... (1)
दिया जाता है कि AX ⊥ DE तथा BD ⊥ DE (वर्ग के आसन्न पक्ष
BDEC)
⇒ BD || AX (एक ही रेखा पर लंबवत दो रेखाएँ एक दूसरे के समानांतर होती हैं)
ΔABD और समांतर चतुर्भुज BYXD एक ही आधार BD पर और समान समांतर रेखाओं BD और AX के बीच स्थित हैं।
∴ ar(ΔABD) = 1/2ar(BYXD)
ar(BYXD) = 2ar(ΔABD)
क्षेत्रफल (BYXD) = 2 क्षेत्र (ΔMBC) [समीकरण (1) का प्रयोग करके] ... (2)
(iii) ΔMBC और समांतर चतुर्भुज ABMN एक ही आधार MB पर और समान समानांतर MB और NC के बीच स्थित हैं।
∴ ar(ΔMBC) = 1/2ar(ABMN)
2ar (ΔMBC) = ar (ABMN)
ar (BYXD) = ar (ABMN) समीकरण (2)] ... (3) का उपयोग करना
(iv) हम जानते हैं कि एक वर्ग का प्रत्येक कोण 90° का होता है।
∴ ∠FCA = ∠BCE = 90º
⇒ ∠FCA + ∠ACB = ∠BCE + ∠ACB
⇒ ∠FCB = ∠ACE
In ΔFCB and ΔACE,
∠FCB = ∠ACE
FC = AC (वर्ग के किनारे ACFG)
CB = CE (वर्ग के किनारे BCED)
ΔFCB ≅ ΔACE (SAS सर्वांगसमता नियम)
(v) यह दिया गया है कि AX ⊥ DE और CE ⊥ DE (वर्ग BDEC की आसन्न भुजाएँ)
इसलिए, CE || AX (एक ही रेखा पर लंबवत दो रेखाएं एक दूसरे के समानांतर हैं)
ΔACE और समांतर चतुर्भुज CYXE पर विचार करें
ΔACE और समांतर चतुर्भुज CYXE एक ही आधार CE पर और एक ही समान्तर रेखाओं CE और AX के बीच स्थित हैं।
∴ ar(ΔACE) = 1/2ar(CYXE)
⇒ ar(CYXE) = 2 ar(ΔACE) ... (4)
हमने साबित कर दिया था कि
∴ ΔFCB ≅ ΔACE
ar (ΔFCB) ≅ ar (ΔACE) ... (5)
समीकरण (4) और (5) की तुलना करने पर, हम प्राप्त करते हैं
ar (CYXE) = 2 ar (ΔFCB) ... (6)
(vi) ΔFCB और समांतर चतुर्भुज ACFG पर विचार करें
ΔFCB और समांतर चतुर्भुज ACFG एक ही आधार CF पर और समान समानांतर CF और BG के बीच स्थित हैं।
∴ ar(ΔFCB) = 1/2 ar(ACFG)
⇒ ar(ACFG) = 2 ar(ΔFCB)
⇒ ar (ACFG) = ar (CYXE) समीकरण का उपयोग करना (6)] ...(7)
(vii) चित्र से स्पष्ट है कि
ar (BCED) = ar (BYXD) + ar (CYXE)
⇒ ar (BCED) = ar (ABMN) + ar (ACFG) [समीकरणों (3) और (7) का उपयोग करना]
APPEARS IN
संबंधित प्रश्न
P और Q एक समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित कोई दो बिंदु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
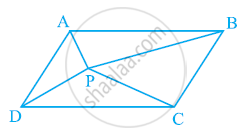
दी गई आकृति में, P एक समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। वो दिखाओ
(i) ar (APB) + ar (PCD) = `1/2`ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[संकेत: के माध्यम से। P, AB के समांतर एक रेखा खींचिए]
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध् के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
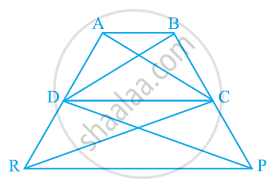
दी गई आकृति में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है | दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब है |
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D, भुजा BC का मध्य-बिंदु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
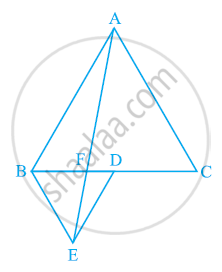
(i) ar (BDE) = `1/4` ar (ABC)
(ii) ar (BDE) = `1/2` ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = `1/8`ar (AFC)
[संकेत : EC और AD को मिलाइए। दिखाओ कि BE || AC and DE || AB, आदि]
चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर काटते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लंब खींचिए।]
निम्नलिखित आकृति में, CD || AE और CY || BA है। सिद्ध कीजिए कि ar (CBX) = ar (AXY) है।
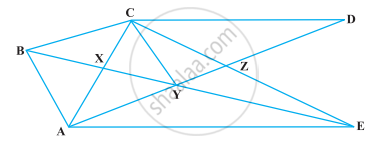
निम्नलिखित आकृति में, X और Y क्रमश : AC और AB के मध्य-बिंदु हैं, QP || BC और CYQ और BXP सरल रेखाएँ हैं। सिद्ध कीजिए कि ar (ABP) = ar (ACQ) हैं।