Advertisements
Advertisements
प्रश्न
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
उत्तर
चूँकि समांतर चतुर्भुज और आयत का आधार और क्षेत्रफल समान है, इसलिए ये भी समान समानांतर रेखाओं के बीच स्थित होंगे।
इस प्रकार समांतर चतुर्भुज ABCD और आयत ABEF पर विचार करें।
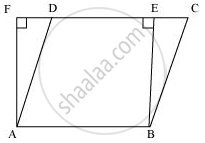
यहाँ, यह देखा जा सकता है कि समांतर चतुर्भुज ABCD और आयत ABEF समान समानांतर AB और CF के बीच हैं।
हम जानते हैं कि एक समांतर चतुर्भुज या एक आयत की सम्मुख भुजाएँ समान लंबाई की होती हैं। इसलिए,
AB = EF (आयताकार के लिए)
AB = CD (समानांतर चतुर्भुज के लिए)
∴ CD = EF
⇒ AB + CD = AB + EF ... (1)
उन सभी रेखाखंडों में से जो किसी बिंदु से उस रेखा तक खींचे जा सकते हैं जो उस पर स्थित नहीं है, लंब रेखा खंड सबसे छोटा है।
∴ AF < AD
और इसी तरह, BE < BC
∴ AF + BE < AD + BC ... (2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
AB + EF + AF + BE < AD + BC + AB + CD
आयत ABEF का परिमाप < समांतर चतुर्भुज ABCD का परिमाप
APPEARS IN
संबंधित प्रश्न
एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। क्षेत्र को कितने भागों में विभाजित किया गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए?
दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है सिद्ध कीजिए कि ABCD एक समलंब है |
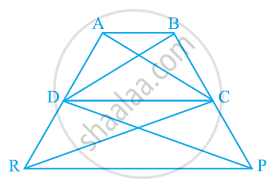
दी गई आकृति में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है | दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब है |
चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर काटते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लंब खींचिए।]
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, रेखाखंड AP का मध्य-बिंदु है, दर्शाइए कि
(i) ar(PRQ) = `1/2` ar(ARC)
(ii) ar(RQC) = `3/8` ar(ABC)
(iii) ar(PBQ) = ar(ARC)
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए : ar (ΔBEF)
एक समांतर चतुर्भुज ABCD के विकर्ण बिंदु O पर प्रतिच्छेद करते हैं। O से होकर एक रेखा खींची जाती है, जो AD को P और BC से Q पर मिलती है। दर्शाइए कि PQ इस समांतर चतुर्भुज ABCD को बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है।
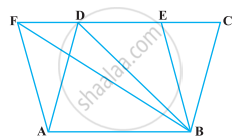
एक त्रिभुज ABC की माध्यिकाएँ BE और CF परस्पर बिंदु G पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∆GBC का क्षेत्रफल चतुर्भुज AFGE के क्षेत्रफल के बराबर हैं।
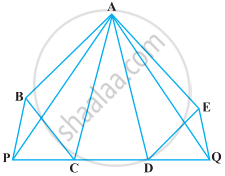
निम्नलिखित आकृति में, ABCDE एक पंचभुज है। AC के समांतर खींची गई BP बढ़ाई गई DC को P पर तथा AD के समांतर खींची गई EQ बढ़ाई गई CD से Q पर मिलती है। सिद्ध कीजिए कि ar (ABCDE) = ar (APQ) है।