Advertisements
Advertisements
प्रश्न
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, रेखाखंड AP का मध्य-बिंदु है, दर्शाइए कि
(i) ar(PRQ) = `1/2` ar(ARC)
(ii) ar(RQC) = `3/8` ar(ABC)
(iii) ar(PBQ) = ar(ARC)
उत्तर
AC पर एक बिंदु S इस प्रकार लें कि S, AC का मध्य-बिंदु हो।
PQ को T तक इस प्रकार बढ़ाइए कि PQ = QT हो।
TC, QS, PS और AQ को मिलाएं।
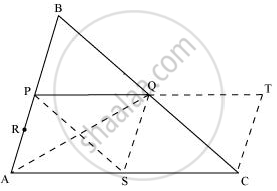
ΔABC में, P और Q क्रमशः AB और BC के मध्य-बिंदु हैं। इसलिए, मध्य-बिंदु सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
PQ || AC और PQ = `1/2`AC
⇒ PQ || AS और PQ = AS (चूंकि S, AC का मध्य-बिंदु है)
∴ PQSA एक समांतर चतुर्भुज है। हम जानते हैं कि एक समांतर चतुर्भुज के विकर्ण उसे त्रिभुजों के बराबर क्षेत्रफलों में समद्विभाजित करते हैं।
∴ ar (ΔPAS) = ar (ΔSQP) = ar (ΔPAQ) = ar (ΔSQA)
इसी प्रकार, यह भी सिद्ध किया जा सकता है कि चतुर्भुज PSCQ, QSCT, और PSQB भी समांतर चतुर्भुज हैं और इसलिए,
ar (ΔPSQ) = ar (ΔCQS) (समांतर चतुर्भुज PSCQ के लिए)
ar (ΔQSC) = ar (ΔCTQ) (समानांतर चतुर्भुज QSCT के लिए)
ar (ΔPSQ) = ar (ΔQBP) (समानांतर चतुर्भुज PSQB के लिए)
इस प्रकार,
ar (ΔPAS) = ar (ΔSQP) = ar (ΔPAQ) = ar (ΔSQA) = ar (ΔQSC) = ar (ΔCTQ) = ar (ΔQBP) ... (1)
साथ ही, ar (ΔABC) = ar (ΔPBQ) + ar (ΔPAS) + ar (ΔPQS) + ar (ΔQSC)
ar (ΔABC) = ar (ΔPBQ) + ar (ΔPBQ) + ar (ΔPBQ) + ar (ΔPBQ)
= 4 ar(ΔPBQ)
ar (ΔPBQ) = 1/4 ar(ΔABC) ... (2)
(i) बिंदु P को C से मिलाइए।
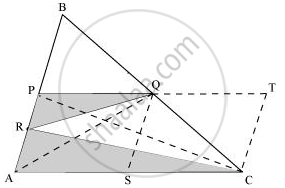
ΔPAQ में, QR माध्यिका है।
`"इसलिए" ar(trianglePRQ)=1/2ar(trianglePAQ)=1/2xx1/4ar(triangleABC)=1/8ar(triangleABC)" ............(3)"`
ΔABC में, P और Q क्रमशः AB और BC के मध्य-बिंदु हैं। इसलिए, मध्य-बिंदु सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
PQ = 1/2AC
AC = 2PQ ⇒ AC = PT
साथ ही, PQ || AC ⇒ PT || AC
अत: PACT एक समांतर चतुर्भुज है।
ar(PACT) = ar(PACQ) + ar(ΔQTC)
= ar (PACQ) + ar (ΔPBQ [समीकरण (1) का प्रयोग करके]
एआर (पीएसीटी) = एआर (ΔABC) ... (4)
∴ `ar(triangleARC) = 1/2ar(trianglePAC)" (CR PAC की माध्यिका है)"`
`= 1/2xx1/2ar(PACT)" (पीसी विकर्ण समांतर चतुर्भुज PACT है)"`
`= 1/4 ar(PACT) = 1/4 ar(triangleABC)`
`rArr 1/2ar(triangleARC) = 1/8ar(triangleABC)`
`rArr1/2ar(triangleARC)=ar(trianglePRQ)" [समीकरण (3) का प्रयोग करते हुए] .........(5)"`
(ii)
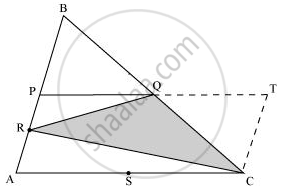
ar(PACT) = ar(ΔPRQ) + ar(ΔARC) + ar(ΔQTC) + ar(ΔRQC)
समीकरणों (1), (2), (3), (4), और (5) से मान रखने पर, हम प्राप्त करते हैं
`ar(ΔABC) = 1/8ar(ΔABC) + 1/4ar(ΔABC) + 1/4ar(ΔABC) + ar(ΔRQC)`
`ar(ΔABC) = 5/8ar(ΔABC) + ar(ΔRQC)`
`ar(ΔRQC) = (1-5/8)ar(ΔABC)`
`ar(ΔRQC) = 3/8ar(ΔABC)`
(iii) समांतर चतुर्भुज PACT में,
`ar(ΔARC) = 1/2ar(ΔPAC)" (CR PAC की माध्यिका है)"`
`= 1/2xx1/2ar(PACT)" (पीसी समांतर चतुर्भुज PACT का विकर्ण है)"`
`= 1/4ar(PACT)`
`= 1/4ar(ABC)`
= ar(ΔPBQ)
APPEARS IN
संबंधित प्रश्न
दी गई आकृति में, P एक समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। वो दिखाओ
(i) ar (APB) + ar (PCD) = `1/2`ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[संकेत: के माध्यम से। P, AB के समांतर एक रेखा खींचिए]
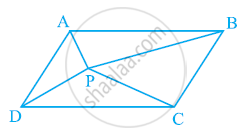
एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। क्षेत्र को कितने भागों में विभाजित किया गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए?
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध् के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है सिद्ध कीजिए कि ABCD एक समलंब है |
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
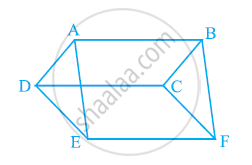
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
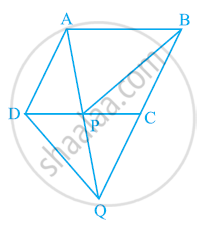
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ)
[संकेत AC को मिलाइए।]
PQRS एक समांतर चतुर्भुज है जिसका क्षेत्रफल 180 cm2 है तथा A विकर्ण QS पर स्थित कोई बिंदु है। तब ∆ASR का क्षेत्रफल 90 cm2 है।
ABCD एक समलंब है, जिसमें AB || DC, DC = 30 cm और AB = 50 cm है। यदि X और Y क्रमश : AD और BC के मध्य-बिंदु हैं, तो सिद्ध कीजिए कि ar (DCYX) = `7/9` ar (XYBA) है।
निम्नलिखित आकृति में, X और Y क्रमश : AC और AB के मध्य-बिंदु हैं, QP || BC और CYQ और BXP सरल रेखाएँ हैं। सिद्ध कीजिए कि ar (ABP) = ar (ACQ) हैं।