Advertisements
Advertisements
प्रश्न
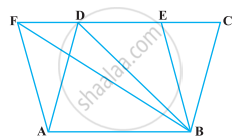
ABCD एक समलंब है, जिसमें AB || DC, DC = 30 cm और AB = 50 cm है। यदि X और Y क्रमश : AD और BC के मध्य-बिंदु हैं, तो सिद्ध कीजिए कि ar (DCYX) = `7/9` ar (XYBA) है।
उत्तर
दिया गया है - एक समलंब ABCD में, AB || DC, DC = 30 सेमी और AB = 50 सेमी है।
साथ ही, X और Y क्रमश : AD और BC के मध्य-बिंदु हैं।
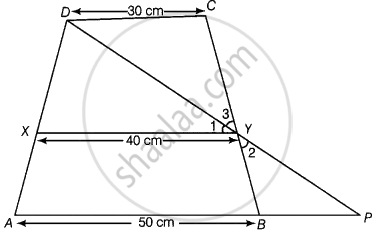
सिद्ध करना है - `ar (DCYX) = 7/9 ar (XYBA)`
रचना - DY से जुड़ें और इसे बढ़ाकर AB को P पर मिलें।
प्रमाण - ΔDCY और ΔPBY में,
CY = BY ...[चूँकि Y, BC का मध्य-बिंदु है।]
∠DCY = ∠PBY ...[चूँकि Y, BC का मध्य-बिंदु है।]
और ∠2 = ∠3 ...[शीर्षाभिमुख कोण]
∴ ΔDCY ≅ ΔPBY ...[ASA सर्वांगसमता नियम द्वारा]
तो, DC = BP ...[CPCT द्वारा]
परंतु DC = 30 cm ...[दिया गया है।]
∴ DC = BP = 30 cm
अब, AP = AB + BP
= 50 + 30
= 80 cm
ΔADP में, मध्य-बिंदु प्रमेय द्वारा,
`XY = 1/2 AP`
= `1/2 xx 80`
= 40 cm
माना AB, XY और XY, DC के बीच की दूरी h सेमी,
अब, समलंब DCYX का क्षेत्रफल = `1/2 h (30 + 40)` ...[∵ समलंब का क्षेत्रफल = `1/2` समानांतर भुजाओं का योग × उनके बीच की दूरी]
= `1/2 h (70)`
= 35 h cm2
इसी तरह, समलंब XYBA का क्षेत्रफल
= `1/2 h (40 + 50)`
= `1/2 h xx 90`
= 45 h cm2
∴ `(ar (DCYX))/(ar (XYBA)) = (35h)/(45h) = 7/9`
⇒ `ar (DCYX) = 7/9 ar (XYBA)`
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
P और Q एक समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित कोई दो बिंदु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढाया गया है | A से होकर CP के समांतर खिंची गई रेखा बढाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है | दर्शाइए कि ar(ABCD) = ar(PBQR) है |
[संकेत: AC और PQ को मिलाइए अब ar(ACQ) और ar(APQ) कि तुलना कीजिये]
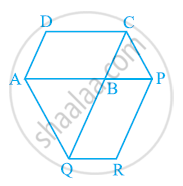
दी गई आकृति में, AP || BQ || CR है | सिद्ध कीजिए कि ar(AQC) = ar(PBR) है |

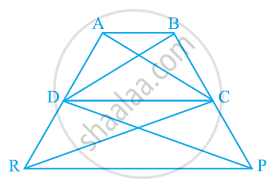
दी गई आकृति में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है | दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब है |
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः BC, CA और AB भुजाओं पर वर्ग हैं। रेखा खंड AX ⊥ DE, भुजा BC से Y पर मिलता है। दर्शाइए कि:
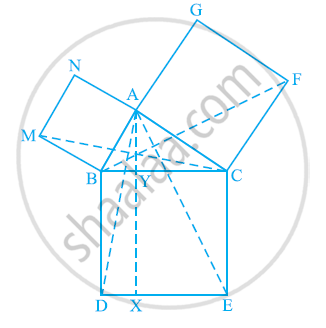
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
नोट: परिणाम (vii) पाइथागोरस का प्रसिद्ध प्रमेय है। आप कक्षा X में इस प्रमेय के सरल प्रमाण के बारे में जानेंगे।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए : ar (ΔBEF)
एक त्रिभुज ABC की माध्यिकाएँ BE और CF परस्पर बिंदु G पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∆GBC का क्षेत्रफल चतुर्भुज AFGE के क्षेत्रफल के बराबर हैं।
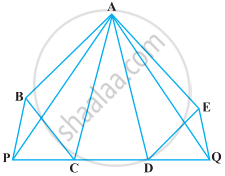
निम्नलिखित आकृति में, ABCDE एक पंचभुज है। AC के समांतर खींची गई BP बढ़ाई गई DC को P पर तथा AD के समांतर खींची गई EQ बढ़ाई गई CD से Q पर मिलती है। सिद्ध कीजिए कि ar (ABCDE) = ar (APQ) है।