Advertisements
Advertisements
प्रश्न
ABCD एक समलंब है, जिसमें AB || DC, DC = 30 cm और AB = 50 cm है। यदि X और Y क्रमश : AD और BC के मध्य-बिंदु हैं, तो सिद्ध कीजिए कि ar (DCYX) = `7/9` ar (XYBA) है।
उत्तर
दिया गया है - एक समलंब ABCD में, AB || DC, DC = 30 सेमी और AB = 50 सेमी है।
साथ ही, X और Y क्रमश : AD और BC के मध्य-बिंदु हैं।
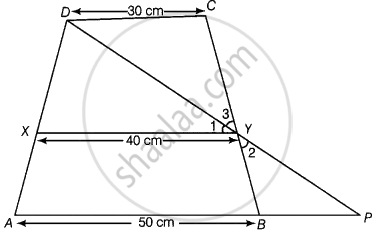
सिद्ध करना है - `ar (DCYX) = 7/9 ar (XYBA)`
रचना - DY से जुड़ें और इसे बढ़ाकर AB को P पर मिलें।
प्रमाण - ΔDCY और ΔPBY में,
CY = BY ...[चूँकि Y, BC का मध्य-बिंदु है।]
∠DCY = ∠PBY ...[चूँकि Y, BC का मध्य-बिंदु है।]
और ∠2 = ∠3 ...[शीर्षाभिमुख कोण]
∴ ΔDCY ≅ ΔPBY ...[ASA सर्वांगसमता नियम द्वारा]
तो, DC = BP ...[CPCT द्वारा]
परंतु DC = 30 cm ...[दिया गया है।]
∴ DC = BP = 30 cm
अब, AP = AB + BP
= 50 + 30
= 80 cm
ΔADP में, मध्य-बिंदु प्रमेय द्वारा,
`XY = 1/2 AP`
= `1/2 xx 80`
= 40 cm
माना AB, XY और XY, DC के बीच की दूरी h सेमी,
अब, समलंब DCYX का क्षेत्रफल = `1/2 h (30 + 40)` ...[∵ समलंब का क्षेत्रफल = `1/2` समानांतर भुजाओं का योग × उनके बीच की दूरी]
= `1/2 h (70)`
= 35 h cm2
इसी तरह, समलंब XYBA का क्षेत्रफल
= `1/2 h (40 + 50)`
= `1/2 h xx 90`
= 45 h cm2
∴ `(ar (DCYX))/(ar (XYBA)) = (35h)/(45h) = 7/9`
⇒ `ar (DCYX) = 7/9 ar (XYBA)`
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। क्षेत्र को कितने भागों में विभाजित किया गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए?
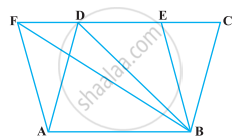
ABCDE एक पंचभुज है| B से होकर AC के समांतर खिंची गई रेखा बढाई गई DC को F पर मिलती है | दर्शाइए कि
(i) ar(ACB) = ar(ACF)
(ii) ar(AEDF) = ar(ABCDE)
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध् के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
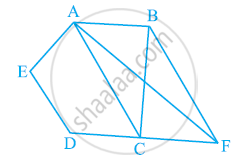
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
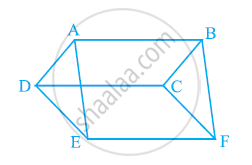
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ)
[संकेत AC को मिलाइए।]
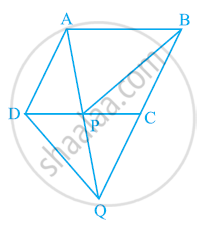
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, रेखाखंड AP का मध्य-बिंदु है, दर्शाइए कि
(i) ar(PRQ) = `1/2` ar(ARC)
(ii) ar(RQC) = `3/8` ar(ABC)
(iii) ar(PBQ) = ar(ARC)
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए : ar (ΔBEF)
किसी समांतर चतुर्भुज ABCD की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती हैं। सिद्ध कीजिए कि ar (ADF) = ar (ABFC) है।
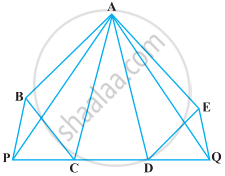
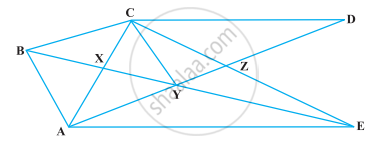
निम्नलिखित आकृति में, CD || AE और CY || BA है। सिद्ध कीजिए कि ar (CBX) = ar (AXY) है।
निम्नलिखित आकृति में, ABCDE एक पंचभुज है। AC के समांतर खींची गई BP बढ़ाई गई DC को P पर तथा AD के समांतर खींची गई EQ बढ़ाई गई CD से Q पर मिलती है। सिद्ध कीजिए कि ar (ABCDE) = ar (APQ) है।