Advertisements
Advertisements
प्रश्न
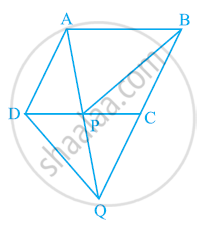
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ)
[संकेत AC को मिलाइए।]
उत्तर
दिया गया है कि ABCD एक समांतर चतुर्भुज है।
AD || BC और AB ||
(समांतर चतुर्भुज की सम्मुख भुजाएँ एक दूसरे के समानांतर होती हैं)
बिंदु A को बिंदु C से मिलाइए।
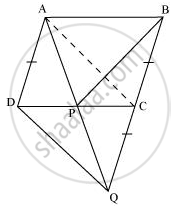
ΔAPC और ΔBPC पर विचार करें
ΔAPC और ΔBPC एक ही आधार PC पर और एक ही समानांतर PC और AB के बीच स्थित हैं। इसलिए,
क्षेत्रफल (ΔAPC) = क्षेत्रफल (ΔBPC) ... (1)
चतुर्भुज ACDQ में, यह दिया गया है कि
AD = CQ
चूँकि ABCD एक समांतर चतुर्भुज है,
एडी || BC (एक समांतर चतुर्भुज की सम्मुख भुजाएँ समान्तर होती हैं)
CQ एक रेखाखंड है जो तब प्राप्त होता है जब रेखाखंड BC बनाया जाता है।
∴ AD || CQ
हमारे पास है,
AC = DQ and AC || DQ
अत: ACQD एक समांतर चतुर्भुज है।
DCQ और ACQ पर विचार करें
ये एक ही आधार CQ पर और एक ही समान्तर रेखाओं CQ और AD के बीच स्थित हैं। इसलिए,
क्षेत्रफल (ΔDCQ) = क्षेत्रफल (ΔACQ)
क्षेत्रफल (ΔDCQ) - क्षेत्रफल (ΔPQC) = क्षेत्रफल (ΔACQ) - क्षेत्रफल (ΔPQC)
क्षेत्रफल (ΔDPQ) = क्षेत्रफल (ΔAPC) ... (2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
क्षेत्रफल (ΔBPC) = क्षेत्रफल (ΔDPQ)
APPEARS IN
संबंधित प्रश्न
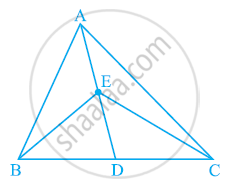
दी गई आकृति में, ΔABC की माध्यिका AD पर स्थित E कोई बिंदु है। दिखाएँ कि ar (ABE) = ar (ACE) है।
दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
बिंदु D और E क्रमश: ΔABC कि भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC) = ar(EBC) है दर्शाइए कि DE || BC है |
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध् के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है सिद्ध कीजिए कि ABCD एक समलंब है |
PQRS एक समांतर चतुर्भुज है जिसका क्षेत्रफल 180 cm2 है तथा A विकर्ण QS पर स्थित कोई बिंदु है। तब ∆ASR का क्षेत्रफल 90 cm2 है।
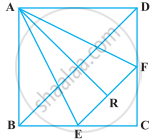
ABCD एक वर्ग है। E और F क्रमश : BC और CD भुजाओं के मध्य-बिंदु हैं। यदि R रेखाखंड EF का मध्य-बिंदु है (आकृति), तो सिद्ध कीजिए कि ar (AER) = ar (AFR) है।
ABCD एक समलंब है, जिसमें AB || DC, DC = 30 cm और AB = 50 cm है। यदि X और Y क्रमश : AD और BC के मध्य-बिंदु हैं, तो सिद्ध कीजिए कि ar (DCYX) = `7/9` ar (XYBA) है।
त्रिभुज ABC में यदि L और M क्रमश : AB और AC भुजाओं पर इस प्रकार स्थित बिंदु हैं कि LM || BC है। सिद्ध कीजिए कि ar (LOB) = ar (MOC) है।
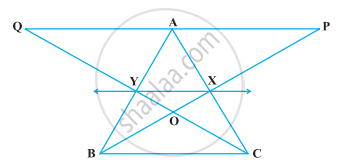
निम्नलिखित आकृति में, X और Y क्रमश : AC और AB के मध्य-बिंदु हैं, QP || BC और CYQ और BXP सरल रेखाएँ हैं। सिद्ध कीजिए कि ar (ABP) = ar (ACQ) हैं।