Advertisements
Advertisements
प्रश्न
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, रेखाखंड AP का मध्य-बिंदु है, दर्शाइए कि
(i) ar(PRQ) = `1/2` ar(ARC)
(ii) ar(RQC) = `3/8` ar(ABC)
(iii) ar(PBQ) = ar(ARC)
उत्तर
AC पर एक बिंदु S इस प्रकार लें कि S, AC का मध्य-बिंदु हो।
PQ को T तक इस प्रकार बढ़ाइए कि PQ = QT हो।
TC, QS, PS और AQ को मिलाएं।
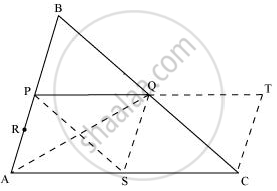
ΔABC में, P और Q क्रमशः AB और BC के मध्य-बिंदु हैं। इसलिए, मध्य-बिंदु सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
PQ || AC और PQ = `1/2`AC
⇒ PQ || AS और PQ = AS (चूंकि S, AC का मध्य-बिंदु है)
∴ PQSA एक समांतर चतुर्भुज है। हम जानते हैं कि एक समांतर चतुर्भुज के विकर्ण उसे त्रिभुजों के बराबर क्षेत्रफलों में समद्विभाजित करते हैं।
∴ ar (ΔPAS) = ar (ΔSQP) = ar (ΔPAQ) = ar (ΔSQA)
इसी प्रकार, यह भी सिद्ध किया जा सकता है कि चतुर्भुज PSCQ, QSCT, और PSQB भी समांतर चतुर्भुज हैं और इसलिए,
ar (ΔPSQ) = ar (ΔCQS) (समांतर चतुर्भुज PSCQ के लिए)
ar (ΔQSC) = ar (ΔCTQ) (समानांतर चतुर्भुज QSCT के लिए)
ar (ΔPSQ) = ar (ΔQBP) (समानांतर चतुर्भुज PSQB के लिए)
इस प्रकार,
ar (ΔPAS) = ar (ΔSQP) = ar (ΔPAQ) = ar (ΔSQA) = ar (ΔQSC) = ar (ΔCTQ) = ar (ΔQBP) ... (1)
साथ ही, ar (ΔABC) = ar (ΔPBQ) + ar (ΔPAS) + ar (ΔPQS) + ar (ΔQSC)
ar (ΔABC) = ar (ΔPBQ) + ar (ΔPBQ) + ar (ΔPBQ) + ar (ΔPBQ)
= 4 ar(ΔPBQ)
ar (ΔPBQ) = 1/4 ar(ΔABC) ... (2)
(i) बिंदु P को C से मिलाइए।
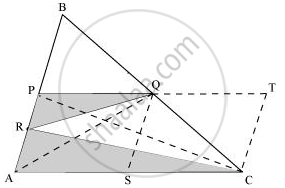
ΔPAQ में, QR माध्यिका है।
`"इसलिए" ar(trianglePRQ)=1/2ar(trianglePAQ)=1/2xx1/4ar(triangleABC)=1/8ar(triangleABC)" ............(3)"`
ΔABC में, P और Q क्रमशः AB और BC के मध्य-बिंदु हैं। इसलिए, मध्य-बिंदु सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
PQ = 1/2AC
AC = 2PQ ⇒ AC = PT
साथ ही, PQ || AC ⇒ PT || AC
अत: PACT एक समांतर चतुर्भुज है।
ar(PACT) = ar(PACQ) + ar(ΔQTC)
= ar (PACQ) + ar (ΔPBQ [समीकरण (1) का प्रयोग करके]
एआर (पीएसीटी) = एआर (ΔABC) ... (4)
∴ `ar(triangleARC) = 1/2ar(trianglePAC)" (CR PAC की माध्यिका है)"`
`= 1/2xx1/2ar(PACT)" (पीसी विकर्ण समांतर चतुर्भुज PACT है)"`
`= 1/4 ar(PACT) = 1/4 ar(triangleABC)`
`rArr 1/2ar(triangleARC) = 1/8ar(triangleABC)`
`rArr1/2ar(triangleARC)=ar(trianglePRQ)" [समीकरण (3) का प्रयोग करते हुए] .........(5)"`
(ii)
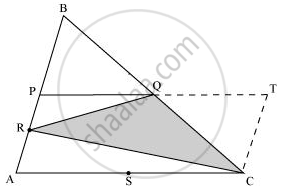
ar(PACT) = ar(ΔPRQ) + ar(ΔARC) + ar(ΔQTC) + ar(ΔRQC)
समीकरणों (1), (2), (3), (4), और (5) से मान रखने पर, हम प्राप्त करते हैं
`ar(ΔABC) = 1/8ar(ΔABC) + 1/4ar(ΔABC) + 1/4ar(ΔABC) + ar(ΔRQC)`
`ar(ΔABC) = 5/8ar(ΔABC) + ar(ΔRQC)`
`ar(ΔRQC) = (1-5/8)ar(ΔABC)`
`ar(ΔRQC) = 3/8ar(ΔABC)`
(iii) समांतर चतुर्भुज PACT में,
`ar(ΔARC) = 1/2ar(ΔPAC)" (CR PAC की माध्यिका है)"`
`= 1/2xx1/2ar(PACT)" (पीसी समांतर चतुर्भुज PACT का विकर्ण है)"`
`= 1/4ar(PACT)`
`= 1/4ar(ABC)`
= ar(ΔPBQ)
APPEARS IN
संबंधित प्रश्न
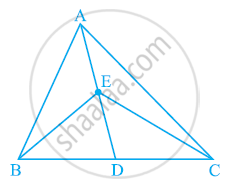
दी गई आकृति में, ΔABC की माध्यिका AD पर स्थित E कोई बिंदु है। दिखाएँ कि ar (ABE) = ar (ACE) है।
बिंदु D और E क्रमश: ΔABC कि भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC) = ar(EBC) है दर्शाइए कि DE || BC है |
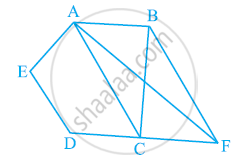
ABCDE एक पंचभुज है| B से होकर AC के समांतर खिंची गई रेखा बढाई गई DC को F पर मिलती है | दर्शाइए कि
(i) ar(ACB) = ar(ACF)
(ii) ar(AEDF) = ar(ABCDE)
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है सिद्ध कीजिए कि ABCD एक समलंब है |
PQRS एक समांतर चतुर्भुज है जिसका क्षेत्रफल 180 cm2 है तथा A विकर्ण QS पर स्थित कोई बिंदु है। तब ∆ASR का क्षेत्रफल 90 cm2 है।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए : ar (ΔBEF)
एक त्रिभुज ABC की माध्यिकाएँ BE और CF परस्पर बिंदु G पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∆GBC का क्षेत्रफल चतुर्भुज AFGE के क्षेत्रफल के बराबर हैं।
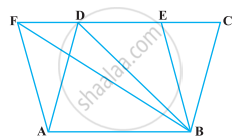
ABCD एक समलंब है, जिसमें AB || DC, DC = 30 cm और AB = 50 cm है। यदि X और Y क्रमश : AD और BC के मध्य-बिंदु हैं, तो सिद्ध कीजिए कि ar (DCYX) = `7/9` ar (XYBA) है।
त्रिभुज ABC में यदि L और M क्रमश : AB और AC भुजाओं पर इस प्रकार स्थित बिंदु हैं कि LM || BC है। सिद्ध कीजिए कि ar (LOB) = ar (MOC) है।
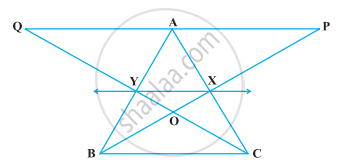
निम्नलिखित आकृति में, X और Y क्रमश : AC और AB के मध्य-बिंदु हैं, QP || BC और CYQ और BXP सरल रेखाएँ हैं। सिद्ध कीजिए कि ar (ABP) = ar (ACQ) हैं।