Advertisements
Advertisements
प्रश्न
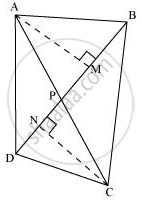
चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर काटते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लंब खींचिए।]
उत्तर
माना AM ⊥ BD और CN ⊥ BD बनाएं
`"त्रिभुज का क्षेत्रफल "=1/2xx"आधार"xx"ऊंचाई"`
`ar(APB)xxar(CPD)=[1/2xxBPxxAM]xx[1/2xxPDxxCN]`
`=1/4xxBPxxAMxxPDxxCN`
`ar(APD)xxar(BPC)=[1/2xxPDxxAM]xx[1/2xxCNxxBP]`
`=1/4xxPDxxAMxxCNxxBP`
`=1/4xxBPxxAMxxPDxxCN`
∴ ar (APB) × ar (CPD) = ar (APD) × ar (BPC)
APPEARS IN
संबंधित प्रश्न
P और Q एक समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित कोई दो बिंदु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। क्षेत्र को कितने भागों में विभाजित किया गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए?
दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
बिंदु D और E क्रमश: ΔABC कि भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC) = ar(EBC) है दर्शाइए कि DE || BC है |
समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढाया गया है | A से होकर CP के समांतर खिंची गई रेखा बढाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है | दर्शाइए कि ar(ABCD) = ar(PBQR) है |
[संकेत: AC और PQ को मिलाइए अब ar(ACQ) और ar(APQ) कि तुलना कीजिये]
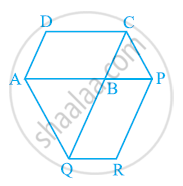
दी गई आकृति में, AP || BQ || CR है | सिद्ध कीजिए कि ar(AQC) = ar(PBR) है |

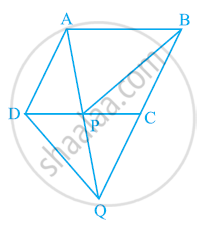
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ)
[संकेत AC को मिलाइए।]
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः BC, CA और AB भुजाओं पर वर्ग हैं। रेखा खंड AX ⊥ DE, भुजा BC से Y पर मिलता है। दर्शाइए कि:
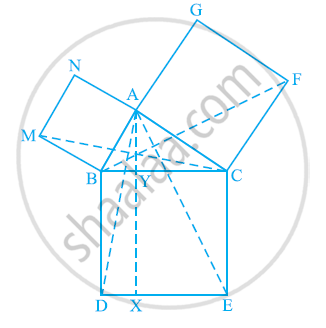
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
नोट: परिणाम (vii) पाइथागोरस का प्रसिद्ध प्रमेय है। आप कक्षा X में इस प्रमेय के सरल प्रमाण के बारे में जानेंगे।
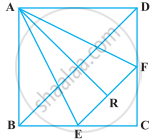
ABCD एक वर्ग है। E और F क्रमश : BC और CD भुजाओं के मध्य-बिंदु हैं। यदि R रेखाखंड EF का मध्य-बिंदु है (आकृति), तो सिद्ध कीजिए कि ar (AER) = ar (AFR) है।
त्रिभुज ABC में यदि L और M क्रमश : AB और AC भुजाओं पर इस प्रकार स्थित बिंदु हैं कि LM || BC है। सिद्ध कीजिए कि ar (LOB) = ar (MOC) है।
