Advertisements
Advertisements
प्रश्न
समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढाया गया है | A से होकर CP के समांतर खिंची गई रेखा बढाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है | दर्शाइए कि ar(ABCD) = ar(PBQR) है |
[संकेत: AC और PQ को मिलाइए अब ar(ACQ) और ar(APQ) कि तुलना कीजिये]
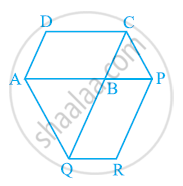
उत्तर
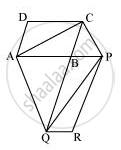
माना AC और PQ को मिलाएँ।
ΔACQ और ΔAQP एक ही आधार AQ पर हैं और समान समानांतर AQ और CP के बीच हैं।
∴ क्षेत्रफल (ΔACQ) = क्षेत्रफल (ΔAPQ)
⇒ क्षेत्रफल (ΔACQ) − क्षेत्रफल (ΔABQ) = क्षेत्रफल (ΔAPQ) − क्षेत्रफल (ΔABQ)
⇒ क्षेत्रफल (ΔABC) = क्षेत्रफल (ΔQBP) ... (1)
चूँकि AC और PQ क्रमशः समांतर चतुर्भुज ABCD और PBQR के विकर्ण हैं,
∴ क्षेत्रफल (ΔABC) = `1/2` क्षेत्रफल (ABCD) ... (2)
क्षेत्रफल (ΔQBP) = `1/2` क्षेत्रफल (PBQR) ... (3)
समीकरण (1), (2), और (3) से, हम प्राप्त करते हैं
`1/2` क्षेत्रफल (ABCD) = `1/2` क्षेत्रफल (PBQR)
क्षेत्रफल (ABCD) = क्षेत्रफल (PBQR)
APPEARS IN
संबंधित प्रश्न
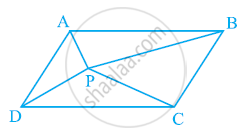
दी गई आकृति में, P एक समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। वो दिखाओ
(i) ar (APB) + ar (PCD) = `1/2`ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[संकेत: के माध्यम से। P, AB के समांतर एक रेखा खींचिए]
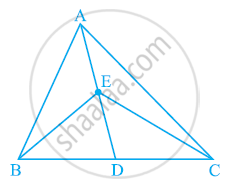
दी गई आकृति में, ΔABC की माध्यिका AD पर स्थित E कोई बिंदु है। दिखाएँ कि ar (ABE) = ar (ACE) है।
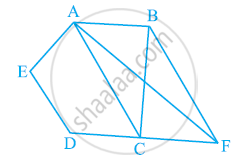
ABCDE एक पंचभुज है| B से होकर AC के समांतर खिंची गई रेखा बढाई गई DC को F पर मिलती है | दर्शाइए कि
(i) ar(ACB) = ar(ACF)
(ii) ar(AEDF) = ar(ABCDE)
दी गई आकृति में, AP || BQ || CR है | सिद्ध कीजिए कि ar(AQC) = ar(PBR) है |

समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
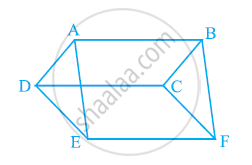
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D, भुजा BC का मध्य-बिंदु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
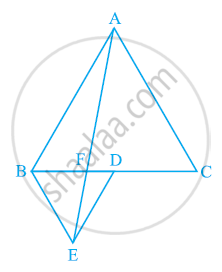
(i) ar (BDE) = `1/4` ar (ABC)
(ii) ar (BDE) = `1/2` ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = `1/8`ar (AFC)
[संकेत : EC और AD को मिलाइए। दिखाओ कि BE || AC and DE || AB, आदि]
चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर काटते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लंब खींचिए।]
एक त्रिभुज ABC की माध्यिकाएँ BE और CF परस्पर बिंदु G पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∆GBC का क्षेत्रफल चतुर्भुज AFGE के क्षेत्रफल के बराबर हैं।
त्रिभुज ABC में यदि L और M क्रमश : AB और AC भुजाओं पर इस प्रकार स्थित बिंदु हैं कि LM || BC है। सिद्ध कीजिए कि ar (LOB) = ar (MOC) है।
