Advertisements
Advertisements
प्रश्न
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
उत्तर
चूँकि समांतर चतुर्भुज और आयत का आधार और क्षेत्रफल समान है, इसलिए ये भी समान समानांतर रेखाओं के बीच स्थित होंगे।
इस प्रकार समांतर चतुर्भुज ABCD और आयत ABEF पर विचार करें।
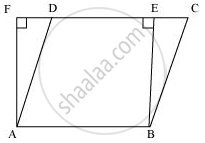
यहाँ, यह देखा जा सकता है कि समांतर चतुर्भुज ABCD और आयत ABEF समान समानांतर AB और CF के बीच हैं।
हम जानते हैं कि एक समांतर चतुर्भुज या एक आयत की सम्मुख भुजाएँ समान लंबाई की होती हैं। इसलिए,
AB = EF (आयताकार के लिए)
AB = CD (समानांतर चतुर्भुज के लिए)
∴ CD = EF
⇒ AB + CD = AB + EF ... (1)
उन सभी रेखाखंडों में से जो किसी बिंदु से उस रेखा तक खींचे जा सकते हैं जो उस पर स्थित नहीं है, लंब रेखा खंड सबसे छोटा है।
∴ AF < AD
और इसी तरह, BE < BC
∴ AF + BE < AD + BC ... (2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
AB + EF + AF + BE < AD + BC + AB + CD
आयत ABEF का परिमाप < समांतर चतुर्भुज ABCD का परिमाप
APPEARS IN
संबंधित प्रश्न
एक त्रिभुज ΔABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = `1/4`ar (ABC) है।
समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढाया गया है | A से होकर CP के समांतर खिंची गई रेखा बढाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है | दर्शाइए कि ar(ABCD) = ar(PBQR) है |
[संकेत: AC और PQ को मिलाइए अब ar(ACQ) और ar(APQ) कि तुलना कीजिये]
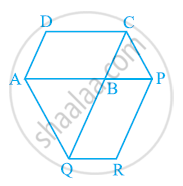
दी गई आकृति में, AP || BQ || CR है | सिद्ध कीजिए कि ar(AQC) = ar(PBR) है |

चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर काटते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लंब खींचिए।]
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, रेखाखंड AP का मध्य-बिंदु है, दर्शाइए कि
(i) ar(PRQ) = `1/2` ar(ARC)
(ii) ar(RQC) = `3/8` ar(ABC)
(iii) ar(PBQ) = ar(ARC)
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए : ar (ΔBEF)
ABCD एक वर्ग है। E और F क्रमश : BC और CD भुजाओं के मध्य-बिंदु हैं। यदि R रेखाखंड EF का मध्य-बिंदु है (आकृति), तो सिद्ध कीजिए कि ar (AER) = ar (AFR) है।
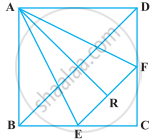
किसी समांतर चतुर्भुज ABCD की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती हैं। सिद्ध कीजिए कि ar (ADF) = ar (ABFC) है।
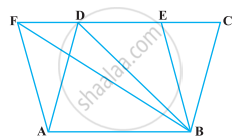
निम्नलिखित आकृति में, CD || AE और CY || BA है। सिद्ध कीजिए कि ar (CBX) = ar (AXY) है।
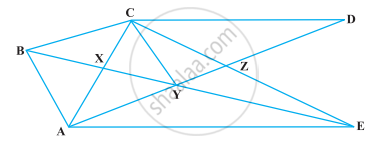
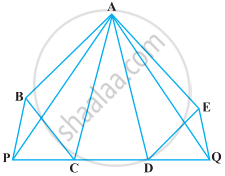
निम्नलिखित आकृति में, ABCDE एक पंचभुज है। AC के समांतर खींची गई BP बढ़ाई गई DC को P पर तथा AD के समांतर खींची गई EQ बढ़ाई गई CD से Q पर मिलती है। सिद्ध कीजिए कि ar (ABCDE) = ar (APQ) है।