Advertisements
Advertisements
Question
ABCD एक समलंब है, जिसमें AB || DC, DC = 30 cm और AB = 50 cm है। यदि X और Y क्रमश : AD और BC के मध्य-बिंदु हैं, तो सिद्ध कीजिए कि ar (DCYX) = `7/9` ar (XYBA) है।
Solution
दिया गया है - एक समलंब ABCD में, AB || DC, DC = 30 सेमी और AB = 50 सेमी है।
साथ ही, X और Y क्रमश : AD और BC के मध्य-बिंदु हैं।
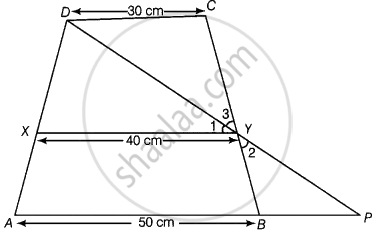
सिद्ध करना है - `ar (DCYX) = 7/9 ar (XYBA)`
रचना - DY से जुड़ें और इसे बढ़ाकर AB को P पर मिलें।
प्रमाण - ΔDCY और ΔPBY में,
CY = BY ...[चूँकि Y, BC का मध्य-बिंदु है।]
∠DCY = ∠PBY ...[चूँकि Y, BC का मध्य-बिंदु है।]
और ∠2 = ∠3 ...[शीर्षाभिमुख कोण]
∴ ΔDCY ≅ ΔPBY ...[ASA सर्वांगसमता नियम द्वारा]
तो, DC = BP ...[CPCT द्वारा]
परंतु DC = 30 cm ...[दिया गया है।]
∴ DC = BP = 30 cm
अब, AP = AB + BP
= 50 + 30
= 80 cm
ΔADP में, मध्य-बिंदु प्रमेय द्वारा,
`XY = 1/2 AP`
= `1/2 xx 80`
= 40 cm
माना AB, XY और XY, DC के बीच की दूरी h सेमी,
अब, समलंब DCYX का क्षेत्रफल = `1/2 h (30 + 40)` ...[∵ समलंब का क्षेत्रफल = `1/2` समानांतर भुजाओं का योग × उनके बीच की दूरी]
= `1/2 h (70)`
= 35 h cm2
इसी तरह, समलंब XYBA का क्षेत्रफल
= `1/2 h (40 + 50)`
= `1/2 h xx 90`
= 45 h cm2
∴ `(ar (DCYX))/(ar (XYBA)) = (35h)/(45h) = 7/9`
⇒ `ar (DCYX) = 7/9 ar (XYBA)`
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
एक त्रिभुज ΔABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = `1/4`ar (ABC) है।
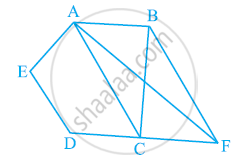
ABCDE एक पंचभुज है| B से होकर AC के समांतर खिंची गई रेखा बढाई गई DC को F पर मिलती है | दर्शाइए कि
(i) ar(ACB) = ar(ACF)
(ii) ar(AEDF) = ar(ABCDE)
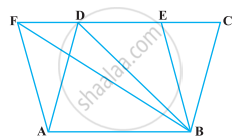
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर काटते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लंब खींचिए।]
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, रेखाखंड AP का मध्य-बिंदु है, दर्शाइए कि
(i) ar(PRQ) = `1/2` ar(ARC)
(ii) ar(RQC) = `3/8` ar(ABC)
(iii) ar(PBQ) = ar(ARC)
PQRS एक समांतर चतुर्भुज है जिसका क्षेत्रफल 180 cm2 है तथा A विकर्ण QS पर स्थित कोई बिंदु है। तब ∆ASR का क्षेत्रफल 90 cm2 है।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए : ar (ΔBEF)
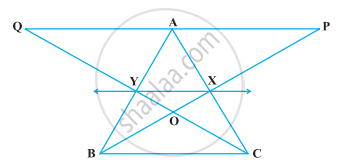
त्रिभुज ABC में यदि L और M क्रमश : AB और AC भुजाओं पर इस प्रकार स्थित बिंदु हैं कि LM || BC है। सिद्ध कीजिए कि ar (LOB) = ar (MOC) है।
निम्नलिखित आकृति में, ABCDE एक पंचभुज है। AC के समांतर खींची गई BP बढ़ाई गई DC को P पर तथा AD के समांतर खींची गई EQ बढ़ाई गई CD से Q पर मिलती है। सिद्ध कीजिए कि ar (ABCDE) = ar (APQ) है।
निम्नलिखित आकृति में, X और Y क्रमश : AC और AB के मध्य-बिंदु हैं, QP || BC और CYQ और BXP सरल रेखाएँ हैं। सिद्ध कीजिए कि ar (ABP) = ar (ACQ) हैं।