Advertisements
Advertisements
प्रश्न
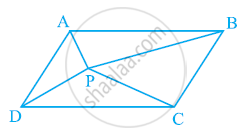
दी गई आकृति में, P एक समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। वो दिखाओ
(i) ar (APB) + ar (PCD) = `1/2`ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[संकेत: के माध्यम से। P, AB के समांतर एक रेखा खींचिए]
उत्तर
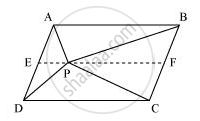
(i) आइए हम एक रेखाखंड EF खींचते हैं, जो बिंदु P से होकर जाता है और रेखाखंड AB के समानांतर है।
समांतर चतुर्भुज ABCD में,
∴ AD || BC (निर्माण द्वारा) ... (1)
ABCD एक समांतर चतुर्भुज है।
एडी || ईसा पूर्व (एक समांतर चतुर्भुज के विपरीत पक्ष)
⇒ AE || BF ... (2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
AB || EF और AE || BF
अत: चतुर्भुज ABFE एक समांतर चतुर्भुज है।
यह देखा जा सकता है कि APB और समांतर चतुर्भुज ABFE एक ही आधार AB पर और समान समानांतर रेखाओं AB और EF के बीच स्थित हैं।
∴ क्षेत्रफल (ΔAPB) = 1/2क्षेत्र (ABFE) ... (3)
इसी प्रकार, ΔPCD और समांतर चतुर्भुज EFCD के लिए,
क्षेत्रफल (ΔPCD) = 1/2क्षेत्र (EFCD) ... (4)
समीकरण (3) और (4) को जोड़ने पर, हम प्राप्त करते हैं
क्षेत्रफल (ΔAPB) + क्षेत्रफल (ΔPCD) = 1/2[क्षेत्रफल (ABFE) + क्षेत्रफल (EFCD)]
क्षेत्रफल (ΔAPB) + क्षेत्रफल (ΔPCD) = 1/2क्षेत्र (ABCD) ........(5)
(ii)
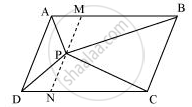
आइए हम एक रेखा खंड MN खींचते हैं, जो बिंदु P से होकर जाता है और रेखा खंड AD के समानांतर है।
समांतर चतुर्भुज ABCD में,
MN || AD (निर्माण द्वारा) ... (6)
ABCD एक समांतर चतुर्भुज है।
एबी || डीसी (एक समांतर चतुर्भुज के विपरीत पक्ष)
AM || DN ... (7)
समीकरण (6) और (7) से, हम प्राप्त करते हैं
MN || AD and AM || DN
अत: चतुर्भुज AMND एक समांतर चतुर्भुज है।
यह देखा जा सकता है कि ΔAPD और समांतर चतुर्भुज AMND एक ही आधार AD पर और समान समानांतर रेखाओं AD और MN के बीच स्थित हैं।
∴ क्षेत्रफल (ΔAPD) = `1/2` क्षेत्र (AMND) ... (8)
इसी तरह, ΔPCB और समानांतर चतुर्भुज MNCB, के लिए,
क्षेत्रफल (ΔPCB) = `1/2` क्षेत्र (MNCB) ... (9)
समीकरण (8) और (9) को जोड़ने पर, हम प्राप्त करते हैं
क्षेत्रफल (ΔAPD) + क्षेत्र (ΔPCB) = `1/2` [क्षेत्रफल (AMND) + क्षेत्रफल (MNCB)]
क्षेत्रफल (ΔAPD) + क्षेत्रफल (ΔPCB) = `1/2` क्षेत्र (ABCD) ............(10)
समीकरणों (5) और (10) की तुलना करने पर, हम प्राप्त करते हैं
क्षेत्रफल (ΔAPD) + क्षेत्रफल (ΔPBC) = क्षेत्रफल (ΔAPB) + क्षेत्रफल (ΔPCD)
APPEARS IN
संबंधित प्रश्न
P और Q एक समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित कोई दो बिंदु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। क्षेत्र को कितने भागों में विभाजित किया गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए?
एक त्रिभुज ΔABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = `1/4`ar (ABC) है।
बिंदु D और E क्रमश: ΔABC कि भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar(DBC) = ar(EBC) है दर्शाइए कि DE || BC है |
दी गई आकृति में, AP || BQ || CR है | सिद्ध कीजिए कि ar(AQC) = ar(PBR) है |

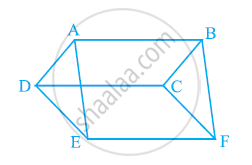
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः BC, CA और AB भुजाओं पर वर्ग हैं। रेखा खंड AX ⊥ DE, भुजा BC से Y पर मिलता है। दर्शाइए कि:
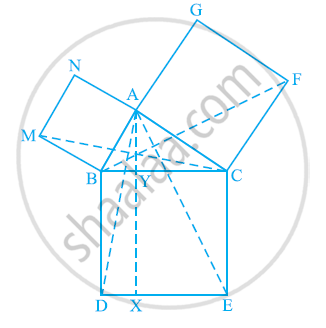
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
नोट: परिणाम (vii) पाइथागोरस का प्रसिद्ध प्रमेय है। आप कक्षा X में इस प्रमेय के सरल प्रमाण के बारे में जानेंगे।
किसी समांतर चतुर्भुज ABCD की भुजा BC पर कोई बिंदु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलती हैं। सिद्ध कीजिए कि ar (ADF) = ar (ABFC) है।
निम्नलिखित आकृति में, ABCDE एक पंचभुज है। AC के समांतर खींची गई BP बढ़ाई गई DC को P पर तथा AD के समांतर खींची गई EQ बढ़ाई गई CD से Q पर मिलती है। सिद्ध कीजिए कि ar (ABCDE) = ar (APQ) है।
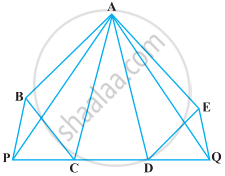
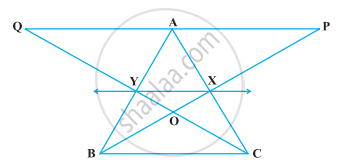
निम्नलिखित आकृति में, X और Y क्रमश : AC और AB के मध्य-बिंदु हैं, QP || BC और CYQ और BXP सरल रेखाएँ हैं। सिद्ध कीजिए कि ar (ABP) = ar (ACQ) हैं।