Advertisements
Advertisements
Question
एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। क्षेत्र को कितने भागों में विभाजित किया गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए?
Solution
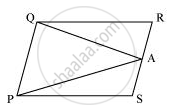
चित्र से यह देखा जा सकता है कि बिंदु A क्षेत्र को तीन भागों में विभाजित करता है। ये भाग आकार में त्रिभुजाकार हैं - ΔPSA, ΔPAQ, और ΔQRA
ΔPSA का क्षेत्रफल + ΔPAQ का क्षेत्रफल + ΔQRA का क्षेत्रफल = PQRS का क्षेत्रफल ... (1)
हम जानते हैं कि यदि एक समांतर चतुर्भुज और एक त्रिभुज एक ही आधार पर और एक ही समांतर रेखाओं के बीच हों, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
∴ क्षेत्रफल (ΔPAQ) = 1/2क्षेत्र (PQRS) ... (2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
क्षेत्रफल (ΔPSA) + क्षेत्रफल (ΔQRA) = `1/2` क्षेत्र (PQRS) ... (3)
स्पष्ट रूप से, यह देखा जा सकता है कि किसान को त्रिकोणीय भाग PAQ में गेहूं और अन्य दो त्रिकोणीय भागों PSA और QRA में दालें या त्रिकोणीय भागों PSA और QRA में गेहूं और त्रिकोणीय भागों PAQ में दालें बोनी चाहिए।
APPEARS IN
RELATED QUESTIONS
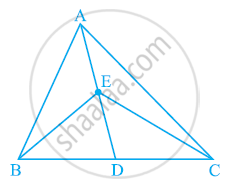
दी गई आकृति में, ΔABC की माध्यिका AD पर स्थित E कोई बिंदु है। दिखाएँ कि ar (ABE) = ar (ACE) है।
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध् के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
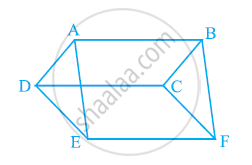
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
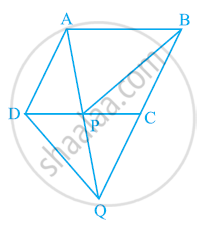
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ)
[संकेत AC को मिलाइए।]
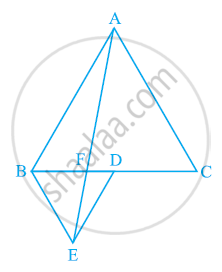
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D, भुजा BC का मध्य-बिंदु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
(i) ar (BDE) = `1/4` ar (ABC)
(ii) ar (BDE) = `1/2` ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = `1/8`ar (AFC)
[संकेत : EC और AD को मिलाइए। दिखाओ कि BE || AC and DE || AB, आदि]
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, रेखाखंड AP का मध्य-बिंदु है, दर्शाइए कि
(i) ar(PRQ) = `1/2` ar(ARC)
(ii) ar(RQC) = `3/8` ar(ABC)
(iii) ar(PBQ) = ar(ARC)
PQRS एक समांतर चतुर्भुज है जिसका क्षेत्रफल 180 cm2 है तथा A विकर्ण QS पर स्थित कोई बिंदु है। तब ∆ASR का क्षेत्रफल 90 cm2 है।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए : ar (ΔBEF)
एक त्रिभुज ABC की माध्यिकाएँ BE और CF परस्पर बिंदु G पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∆GBC का क्षेत्रफल चतुर्भुज AFGE के क्षेत्रफल के बराबर हैं।
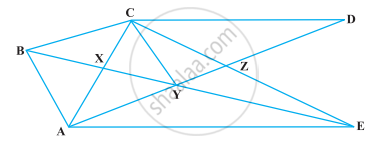
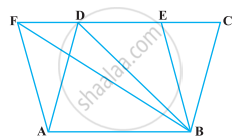
निम्नलिखित आकृति में, CD || AE और CY || BA है। सिद्ध कीजिए कि ar (CBX) = ar (AXY) है।