Advertisements
Advertisements
Question
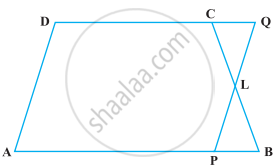
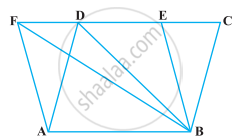
एक समलंब ABCD में, AB || DC है तथा L भुजा BC का मध्य-बिंदु है। L से होकर, एक रेखा PQ || AD खींची गई है, जो AB को P पर और बढ़ाई गई DC को Q पर मिलती है (आकृति), सिद्ध कीजिए ar (ABCD) = ar (APQD)
Solution
दिया गया है - समलंब ABCD में, AB || DC, DC Q में उत्पादित और L, BC का मध्य-बिंदु है।
∴ BL = CL
सिद्ध करना है - ar (ABCD) = ar (APQD)
प्रमाण - चूँकि, DC का उत्पादन Q में होता है और AB || DC।
तो, DQ || AB
ΔCLQ और ΔBLP में,
CL = BL ...[चूँकि L, BC का मध्य-बिंदु है।]
∠LCQ = ∠LBP ...[वैकल्पिक आंतरिक कोण क्योंकि BC एक तिर्यक रेखा है।]
∠CQL = ∠LPB ...[वैकल्पिक आंतरिक कोण, क्योंकि PQ एक तिर्यक रेखा है।]
∴ ΔCLQ ≅ ΔBLP ...[AAS सर्वांगसमता नियम द्वारा]
तब, ar (ΔCLQ) = ar (ΔBLP) [चूँकि, सर्वांगसम त्रिभुजों का क्षेत्रफल बराबर होता है।] ...(i)
अब, ar (ABCD) = ar (APQD) – ar (ΔCQL) + ar (ΔBLP)
= ar (APQD) – ar (ΔBLP) + ar (ΔBLP) ...[समीकरण (i) से]
⇒ ar (ABCD) = ar (APQD)
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
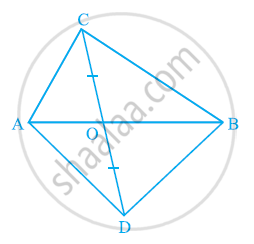
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है | यदि AB = CD है, तो दर्शाइए की
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है |
[संकेत: D और B से AC पर लंब खींचिए।]

ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
निम्नलिखित आकृतियों में से किसमें आप एक ही आधार पर और एक ही समांतर रेखाओं के बीच, बने दो बहुभुज प्राप्त करते हैं :
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिंदुओं को मिलाने से बनी आकृति है :
निम्नलिखित आकृति में, यदि समांतर चतुर्भुज ABCD और आयत ABEM समान क्षेत्रफल के हैं, तो ______।
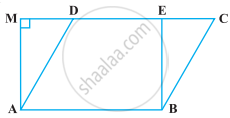
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD ______।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए :
ar (ΔABD)
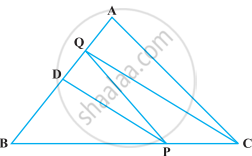
∆ABC, D भुजा AB का मध्य-बिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखंड CQ || PD भुजा AB से Q पर मिलता है (आकृति), तो सिद्ध कीजिए कि ar (BPQ) = `1/2` ar (∆ABC) है।
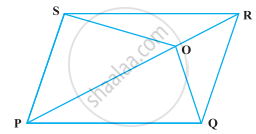
O एक समांतर चतुर्भुज PQRS के विकर्ण PR पर स्थित कोई बिंदु है (आकृति)। सिद्ध कीजिए कि ar (PSO) = ar (PQO) है।