Advertisements
Advertisements
प्रश्न
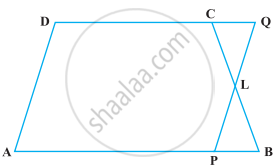
एक समलंब ABCD में, AB || DC है तथा L भुजा BC का मध्य-बिंदु है। L से होकर, एक रेखा PQ || AD खींची गई है, जो AB को P पर और बढ़ाई गई DC को Q पर मिलती है (आकृति), सिद्ध कीजिए ar (ABCD) = ar (APQD)
उत्तर
दिया गया है - समलंब ABCD में, AB || DC, DC Q में उत्पादित और L, BC का मध्य-बिंदु है।
∴ BL = CL
सिद्ध करना है - ar (ABCD) = ar (APQD)
प्रमाण - चूँकि, DC का उत्पादन Q में होता है और AB || DC।
तो, DQ || AB
ΔCLQ और ΔBLP में,
CL = BL ...[चूँकि L, BC का मध्य-बिंदु है।]
∠LCQ = ∠LBP ...[वैकल्पिक आंतरिक कोण क्योंकि BC एक तिर्यक रेखा है।]
∠CQL = ∠LPB ...[वैकल्पिक आंतरिक कोण, क्योंकि PQ एक तिर्यक रेखा है।]
∴ ΔCLQ ≅ ΔBLP ...[AAS सर्वांगसमता नियम द्वारा]
तब, ar (ΔCLQ) = ar (ΔBLP) [चूँकि, सर्वांगसम त्रिभुजों का क्षेत्रफल बराबर होता है।] ...(i)
अब, ar (ABCD) = ar (APQD) – ar (ΔCQL) + ar (ΔBLP)
= ar (APQD) – ar (ΔBLP) + ar (ΔBLP) ...[समीकरण (i) से]
⇒ ar (ABCD) = ar (APQD)
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
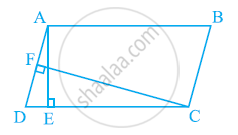
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
यदि E, F, G और H क्रमशः एक समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = `1/2`ar (ABCD) हैं
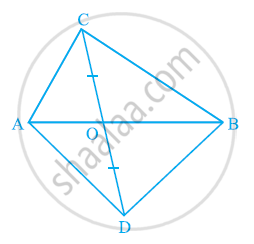
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
एक समलंब ABCD, जिसमें AB || DC हैं, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दर्शाइए कि ar(AOD) = ar(BOC) है |
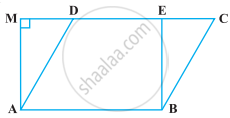
निम्नलिखित आकृति में, यदि समांतर चतुर्भुज ABCD और आयत ABEM समान क्षेत्रफल के हैं, तो ______।
एक त्रिभुज की भुजाओं के मध्य-बिंदु किसी भी एक शीर्ष को चौथा बिंदु लेकर एक समांतर चतुर्भुज बनाते हैं, जिसका क्षेत्रफल बराबर है
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD ______।
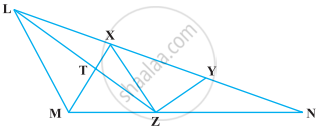
X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार हैं कि LX = XY = YN हैं। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। (देखिए आकृति)। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है (आकृति)। ज्ञात कीजिए :
- ar (ABEF)
- ar (ABD)
- ar (BEF)