Advertisements
Advertisements
Question
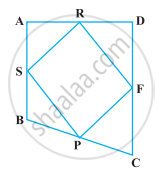
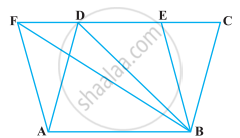
यदि किसी चतुर्भुज की भुजाओं के मध्य-बिंदुओं को क्रम से मिलाया जाता है, तो सिद्ध कीजिए कि इस प्रकार बने समांतर चतुर्भुज का क्षेत्रफल दिए हुए चतुर्भुज के क्षेत्रफल का आधा होता है (आकृति)।
[संकेत : BD को मिलाइए और A से BD पर लंब खींचिए।]
Solution
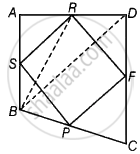
दिया गया है - मान लीजिए ABCD एक चतुर्भुज है और P, F, R और S क्रमशः भुजाओं BC, CD, AD और AB के मध्य-बिंदु हैं और PFRS एक समांतर चतुर्भुज है।
सिद्ध करना है - ar (समांतर चतुर्भुज PFRS) = `1/2` ar (चतुर्भुज ABCD)
रचना - BD और BR को मिलाइए।
उपपत्ति - माध्यिका BR, ΔBDA को समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
∴ ar (ΔBRA) = `1/2` ar (ΔBDA) ...(i)
इसी प्रकार, माध्यिका RS, ΔBRA को समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
∴ ar (ΔASR) = `1/2` ar (ΔBRA) ...(ii)
समीकरण (i) और (ii) से,
ar (ΔASR) = `1/4` ar (ΔBDA) ...(iii)
इसी प्रकार, ar (ΔCFP) = `1/4` ar (ΔBCD) ...(iv)
समीकरण (iii) और (iv) को जोड़ने पर, हम पाते हैं।
ar (ΔASR) + ar (ΔCFP) = `1/4` ar (ΔBDA) ...[ar (ΔBDA) + ar (ΔBCD)]
⇒ ar (ΔASR) + ar (ΔCFP) = `1/4` ar (चतुर्भुज BCDA) ...(v)
इसी प्रकार, ar (ΔDRF) + ar (ΔBSP) = `1/4` ar (चतुर्भुज BCDA) ...(vi)
समीकरण (v) और (vi) को जोड़ने पर, हम पाते हैं।
ar (ΔASR) + ar (ΔCFP) + ar (ΔDRF) + ar (ΔBSP) = `1/2` ar (चतुर्भुज BCDA) ...(vii)
लेकिन ar (ΔASR) + ar (ΔCFP) + ar (ΔDRF) + ar (ΔBSP) + ar (समांतर चतुर्भुज PFRS) = ar (चतुर्भुज BCDA) ...(viii)
समीकरण (vii) को समीकरण (viii) से घटाने पर, हम पाते हैं।
ar (समांतर चतुर्भुज PFRS) = `1/2` ar (चतुर्भुज BCDA)
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
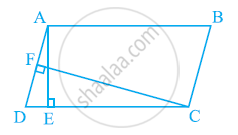
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप इस प्रश्न का उत्तर दे सकते हैं कि आपने इस अध्याय के 'परिचय' में छोड़ दिया है कि "क्या बुधिया के खेत को वास्तव में बराबर क्षेत्रफल के तीन भागों में बांटा गया है"?
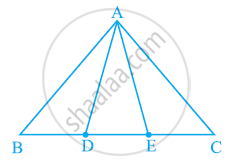
[टिप्पणी: ध्यान दें कि BD = DE = EC लेने पर त्रिभुज ABC को बराबर क्षेत्रफलों वाले तीन त्रिभुज ABD, ADE और AEC में विभाजित किया जाता है। इसी तरह, BC को n समान भागों में विभाजित करके और इस प्रकार प्राप्त विभाजन बिंदुओं को BC के विपरीत शीर्ष से जोड़कर, आप ΔABC को समान क्षेत्रफल वाले n त्रिभुजों में विभाजित कर सकते हैं।]
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल है :
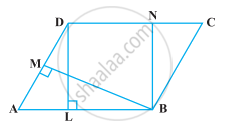
निम्नलिखित आकृति में, यदि समांतर चतुर्भुज ABCD और आयत ABEM समान क्षेत्रफल के हैं, तो ______।
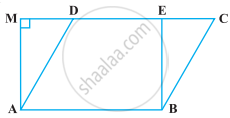
एक त्रिभुज की भुजाओं के मध्य-बिंदु किसी भी एक शीर्ष को चौथा बिंदु लेकर एक समांतर चतुर्भुज बनाते हैं, जिसका क्षेत्रफल बराबर है
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। तब, ar (BDE) = `1/4` ar (ABC) है।
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
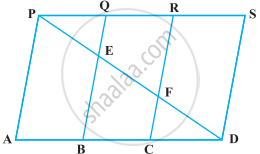
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है (आकृति)। ज्ञात कीजिए :
- ar (ABEF)
- ar (ABD)
- ar (BEF)
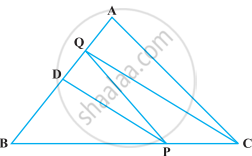
∆ABC, D भुजा AB का मध्य-बिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखंड CQ || PD भुजा AB से Q पर मिलता है (आकृति), तो सिद्ध कीजिए कि ar (BPQ) = `1/2` ar (∆ABC) है।