Advertisements
Advertisements
Question
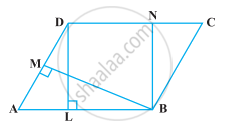
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल है :
Options
AB × BM
BC × BN
DC × DL
AD × DL
Solution
DC × DL
स्पष्टीकरण -

हम जानते हैं कि, एक समांतर चतुर्भुज का क्षेत्रफल उसकी किसी भी भुजा और संबंधित ऊँचाई (या ऊँचाई) का गुणनफल होता है।
यहाँ, जब AB आधार है, तो शीर्षलंब DL है।
समांतर चतुर्भुज का क्षेत्रफल = AB × DL और जब AD आधार है, तो ऊँचाई BM है।
समांतर चतुर्भुज का क्षेत्रफल = AD × BM जब DC आधार है, तो ऊँचाई DL है।
समांतर चतुर्भुज का क्षेत्रफल = DC × DL और जब BC आधार हो, तो ऊँचाई नहीं दी जाती है।
APPEARS IN
RELATED QUESTIONS
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
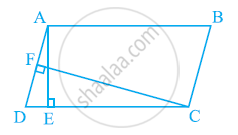
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
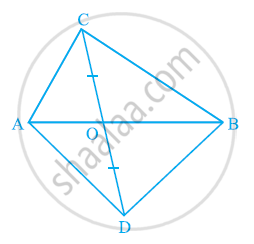
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है | यदि AB = CD है, तो दर्शाइए की
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है |
[संकेत: D और B से AC पर लंब खींचिए।]

ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप इस प्रश्न का उत्तर दे सकते हैं कि आपने इस अध्याय के 'परिचय' में छोड़ दिया है कि "क्या बुधिया के खेत को वास्तव में बराबर क्षेत्रफल के तीन भागों में बांटा गया है"?
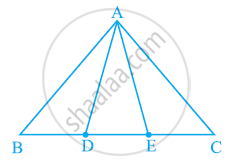
[टिप्पणी: ध्यान दें कि BD = DE = EC लेने पर त्रिभुज ABC को बराबर क्षेत्रफलों वाले तीन त्रिभुज ABD, ADE और AEC में विभाजित किया जाता है। इसी तरह, BC को n समान भागों में विभाजित करके और इस प्रकार प्राप्त विभाजन बिंदुओं को BC के विपरीत शीर्ष से जोड़कर, आप ΔABC को समान क्षेत्रफल वाले n त्रिभुजों में विभाजित कर सकते हैं।]
निम्नलिखित आकृतियों में से किसमें आप एक ही आधार पर और एक ही समांतर रेखाओं के बीच, बने दो बहुभुज प्राप्त करते हैं :
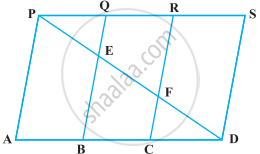
निम्नलिखित आकृति में, PSDA एक समांतर चतुर्भुज है। PS पर बिंदु Q और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि ar (PQE) = ar (CFD) है।
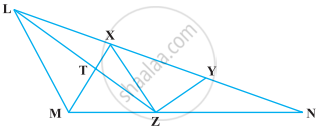
X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार हैं कि LX = XY = YN हैं। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। (देखिए आकृति)। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।
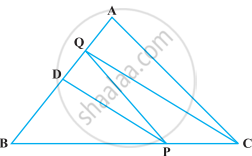
∆ABC, D भुजा AB का मध्य-बिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखंड CQ || PD भुजा AB से Q पर मिलता है (आकृति), तो सिद्ध कीजिए कि ar (BPQ) = `1/2` ar (∆ABC) है।
एक समलंब ABCD में, AB || DC है तथा L भुजा BC का मध्य-बिंदु है। L से होकर, एक रेखा PQ || AD खींची गई है, जो AB को P पर और बढ़ाई गई DC को Q पर मिलती है (आकृति), सिद्ध कीजिए ar (ABCD) = ar (APQD)