Advertisements
Advertisements
प्रश्न
Derive the relationship between the peak and the rms value of current in an a.c. circuit.
उत्तर
The instantaneous power dissipated in the resistor is`p = i^2 R = i_m^2 sin^2 omegat`
The average value of p over a cycle is:
`p = <i^2R> =<i_m^2 R sin^2 omegat>`
`i_m^2 and R` are constants. Therefore,
`p = i_m^2 R<sin^2 omegat>`
By trigonometric identity,
`sin^2 omegat = 1/2 (1-cos2 omegat)`
Then,
`<sin^2 omegat > =1/2 (1- <cos2omegat>)`
The average value of cos 2 ωt is zero.
We have:
`< sin^2 omegat > =1/2 (1-0)`
`< sin^2 omegat> =1/2`
Thus,
`P = 1/2 i_m^2`
The rms value in the ac power is expressed in the same form as dc power root mean square or effective current and is denoted by Irms.
Peak current is `i_m`
Therefore,
`I = (i_m)/sqrt2 =0.707 i_m`
`I^2 R = (i_m^2)/2 R`
`I = i_m/sqrt2`
APPEARS IN
संबंधित प्रश्न
In a series RL circuit, the resistance and inductive reactance are the same. Then the phase difference between the voltage and current in the circuit is
What do you mean by resonant frequency?
When does power factor of a series RLC circuit become maximum?
A 60 µF capacitor is connected to a 110 V, 60 Hz ac supply. Determine the rms value of the current in the circuit.
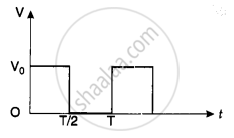
The rms value of potential difference V shown in the figure is ______.
Which of the following graphs represent the variation of current(I) with frequency (f) in an AC circuit containing a pure capacitor?
An alternating voltage source of variable angular frequency ‘w’ and fixed amplitude ‘V’ is connected in series with a capacitance C and electric bulb of resistance R(inductance zero). When ‘w’ is increased ______.
In an alternating current circuit consisting of elements in series, the current increases on increasing the frequency of supply. Which of the following elements are likely to constitute the circuit?
- Only resistor.
- Resistor and an inductor.
- Resistor and a capacitor.
- Only a capacitor.
An inductor of 0.5 mH, a capacitor of 200 µF, and a resistor of 2Ω are connected in series with a 220V ac source. If the current is in phase with the emf, the frequency of ac source will be ______ × 102 Hz.
