Advertisements
Advertisements
प्रश्न
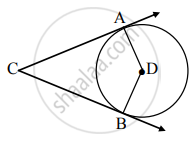
दिलेल्या आकृतीत, केंद्र D असलेले वर्तुळ ∠ACB च्या बाजूंना बिंदू A आणि B मध्ये स्पर्श करते. जर ∠ACB = 52°, तर ∠ADB चे माप काढा.
उत्तर
∴ ∠ACB + ∠CAD + ∠CBD + ∠ADB = 360° ...[चौकोनाच्या सर्व कोनांच्या मापांची बेरीज 360° असते.]
∴ 52° + 90° + 90° + ∠ADB = 360° ...[स्पर्शिका-त्रिज्या प्रमेय]
∴ ∠ADB + 232° = 360°
∴ ∠ADB = 360° – 232°
= 128°
संबंधित प्रश्न
त्रिज्या 4.5 सेमी असलेल्या वर्तुळाच्या दोन स्पर्शिका परस्परांना समांतर आहेत. तर त्या स्पर्शिकांतील अंतर किती हे सकारण लिहा.
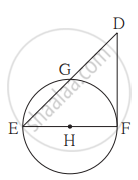
आकृती मध्ये, रेख EF हा व्यास आणि रेख DF हा स्पर्शिकाखंड आहे. वर्तुळाची त्रिज्या r आहे. तर सिद्ध करा - DE × GE = 4r2
एका वर्तुळाच्या केंद्रापासून 12.5 सेमी अंतरावरील एका बिंदूतून त्या वर्तुळाला काढलेल्या स्पर्शिकाखंडाची लांबी 12 सेमी आहे. तर त्या वर्तुळाचा व्यास किती सेमी आहे?
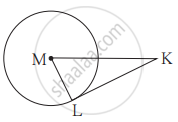
सोबतच्या आकृतीत, बिंदू M वर्तुळकेंद्र आणि रेख KL हा स्पर्शिकाखंड आहे. जर MK = 12, KL = `6sqrt3` तर
(1) वर्तुळाची त्रिज्या काढा.
(2) ∠K आणि ∠M यांची मापे ठरवा.
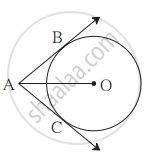
आकृती मध्ये, बिंदू O वर्तुळकेंद्र आणि रेख AB व रेख AC हे स्पर्शिकाखंड आहेत. जर वर्तुळाची त्रिज्या r असेल आणि l(AB) = r असेल, तर `square`ABOC हा चौरस होतो, हे दाखवा.
शेजारील आकृतीत, रेषा l ही केंद्र O असलेल्या वर्तुळाला बिंदू P मध्ये स्पर्श करते. बिंदू Q हा त्रिज्या OP चा मध्यबिंदू आहे. बिंदू Q ला सामावणारी जीवा RS || रेषा l. जर RS 12 सेमी असेल, तर वर्तुळाची त्रिज्या काढा.
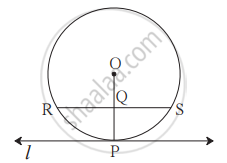
शेजारील आकृतीत, रेषा l ही केंद्र O असलेल्या वर्तुळाला बिंदू P मध्ये स्पर्श करते. बिंदू Q हा त्रिज्या OP चा मध्यबिंदू आहे. बिंदू Q ला सामावणारी जीवा RS || रेषा l. जर RS 12 सेमी असेल, तर वर्तुळाची त्रिज्या काढा.

शेजारील आकृतीत, रेषा l ही केंद्र O असलेल्या वर्तुळाला बिंदू P मध्ये स्पर्श करते. बिंदू Q हा त्रिज्या OP चा मध्यबिंदू आहे. बिंदू Q ला सामावणारी जीवा RS || रेषा l. जर RS 12 सेमी असेल, तर वर्तुळाची त्रिज्या काढा.

आकृती मध्ये, केंद्र C असलेल्या वर्तुळाचा रेख AB हा व्यास आहे. वर्तुळाची स्पर्शिका PQ वर्तुळाला बिंदू T मध्ये स्पर्श करते. रेख AP ⊥ रेषा PQ आणि रेख BQ ⊥ रेषा PQ. तर सिद्ध करा - रेख CP ≅ रेख CQ.
आकृतीत रेख RM आणि रेख RN हे केंद्र O असलेल्या वर्तुळाचे स्पर्शिका खंड आहेत, तर रेख OR हा ∠MRN आणि ∠MON या दोन्ही कोनांचा दुभाजक आहे, हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
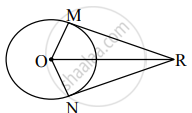
सिद्धता:
ΔRMO आणि ΔRNO यांमध्ये,
∠RMO ≅ ∠RNO = 90° ...............[`square`]
कर्ण OR ≅ कर्ण OR …..............[`square`]
बाजू OM ≅ बाजू [`square`] ..........…[एकाच वर्तुळाच्या त्रिज्या]
∴ ΔRMO ≅ ΔRNO ….......[`square`]
∠MOR ≅ ∠NOR
तसेच, ∠MRO ≅ [`square`] ......................[`square`]
∴ रेख OR ∠MRN आणि ∠MON या दोन्ही कोनांची दुभाजक आहे.
