Advertisements
Advertisements
प्रश्न
Draw an angle of 110° with the help of a protractor and bisect it. Measure each angle.
उत्तर
Draw ∠BXA = 110° with the help of a protractor.
Now, we use the following steps for required construction
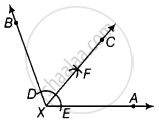
1. Taking X as centre and any radius draw an arc to intersect the rays XA and XB, say at E and D, respectively.
2. Taking D and E as centres and with the radius more than `1/2` DE, draw arcs to intersect each other, say at F.
3. Draw the ray XF. Thus, ray XF is the required bisector of the angle BXA. On measuring each angle, we get
∠BXC = ∠AXC = 55° ...[∴ ∠BXC = ∠AXC = `1/2` ∠BXA = `1/2` × 110° = 55°]
APPEARS IN
संबंधित प्रश्न
Construct the 75° angles and verify by measuring it by a protractor.
Construct the 135° angles and verify by measuring it by a protractor.
Construct an equilateral triangle, given its side and justify the construction.
Draw a line segment AB of length 5.8 cm. Draw the perpendicular bisector of this line
segment.
Draw a circle with centre at point O. Draw its two chords AB and CD such that AB is not
parallel to CD. Draw the perpendicular bisectors of AB and CD. At what point do they
intersect?
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line.
Using ruler and compasses only, draw an angle of measure 135°.
Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Construct the following angles at the initial point of a given ray and justify the construction 45°
