Advertisements
Advertisements
प्रश्न
Draw a neat labelled diagram of Young’s Double Slit experiment. Show that `beta = (lambdaD)/d` , where the terms have their usual meanings (either for bright or dark fringe).
उत्तर

`PM_1 = x - d/2 and PM_2 = x + d/2`
In `DeltaS_2M_2P`
`(S_2P)^2 = (S_2M_2)^2 + (PM_2)^2`
`therefore (S_2P)^2 = D^2 + (x + d/2)^2` ....(i)
In `DeltaS_1M_1P`
`(S_1P)^2 = (S_1M_1)^2 + (PM_1)^2`
`therefore (S_1P)^2 = D^2 + (x - d/2)^2` ....(ii)
`(S_2P)^2 - (S_1P)^2 = D^2 + (x + d/2)^2 - D^2 - (x - d/2)^2`
`(S_2P - S_1P)(S_2P + S_1P) = x^2 + xd + d^2/4 - x^2 + xd - d^2/4`
`therefore S_2P - S_1P = (2xd)/(S_2P + S_1P)`
In practice, the distances x and d are very small as compared to D. To a first approximation we can write
`S_1P = S_2P = D or S_2P + S_1P = 2D`
`therefore` The path difference between two waves is given by
`S_2P - S_1P = (2xd)/(2D) = (xd)/D` .....(iii)
Now the intensity at P will be maximum or minimum according to the path difference. The point P will be bright if the path difference is an even multiple of `lambda/2` .
i.e. `S_2P - S_1P = (xd)/D = 2n(lambda/2)` ....(iv)
where n = 0,1,2,3, ...........
Or `x = n(lambdaD)/d` ....(v)
The Point P will be dark if the path difference is an odd multiple of
i.e. `S_2P - S_1P = (xd)/D = (2m - 1)lambda/2` ...(vi)
where m = 1,2,3, ...............
Or `x = (2m - 1) (lambdaD)/(2d)` ....(vii)
Expression for the band (fringe) width
The distance between the center of two adjcent bright or dark bands is called band width or fringe width.
Let `X_n` and `X_n+1` denotes the distances of `n^(th)` and `(n+1)^(th)` bright band on the same side of central
bright band, then from equation (v)
`X_n = n(lambdaD)/d`
`X_(n+1) = (n+1)(lambdaD)/d`
`X_(n+1) - X_n = (n+1-n)(lambdaD)/d`
`therefore beta = (lambdaD)/d` ...(viii)
APPEARS IN
संबंधित प्रश्न
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
Write two characteristics features distinguish the diffractions pattern from the interference fringes obtained in Young’s double slit experiment.
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
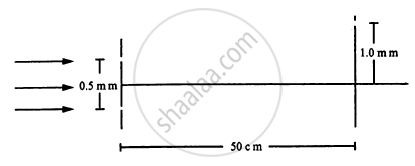
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
In Young's double-slit experiment, the two slits are separated by a distance of 1.5 mm, and the screen is placed 1 m away from the plane of the slits. A beam of light consisting of two wavelengths of 650 nm and 520 nm is used to obtain interference fringes.
Find the distance of the third bright fringe for λ = 520 nm on the screen from the central maximum.
"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit".
Justify the above statement through a relevant mathematical expression.
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
