Advertisements
Advertisements
प्रश्न
Draw ΔRSP ∼ ΔTQP. In ΔTQP, TP = 5 cm, ∠P = 50°, PQ = 4.5 cm and `("RS")/("TQ") = 2/3`.
उत्तर
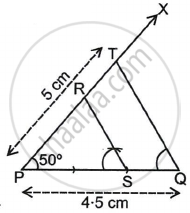
Steps of construction:
- Draw segment PQ = 4.5 cm.
- Draw ray PX such that ∠XPQ = 50°.
- Take point T on ray PX such that PT = 5 cm.
- Join TQ. ΔTQP is obtained.
- Divide segment PQ into 3 equal parts.
- Fix point S on PQ such that the length of PS is `2/3` of the length of segment PQ.
- Draw a line parallel to side TQ through S.
- Name the point of intersection of the line and ray PT as R. Thus, we get the required ΔRSP similar to ΔTQP.
APPEARS IN
संबंधित प्रश्न
Draw an equilateral ΔABC with side 6.2 cm and construct its circumcircle
Find the length of the altitude of an equilateral triangle with side 6 cm.
∆ABC ~ ∆LMN. In ∆ABC, AB = 5.5 cm, BC = 6 cm, CA = 4.5 cm. Construct ∆ABC and ∆LMN such that `"BC"/"MN" = 5/4`.
∆RST ~ ∆XYZ. In ∆RST, RS = 4.5 cm, ∠RST = 40°, ST = 5.7 cm Construct ∆RST and ∆XYZ, such that \[\frac{RS}{XY} = \frac{3}{5} .\]
Draw a triangle ABC with side BC = 6cm, ∠B = 45° and ∠A = 100°, then construct a triangle PBQ whose sides are `7/4` times the corresponding sides of ΔABC.
Choose the correct alternative:
ΔLMN ~ ΔHIJ and `"LM"/"HI" = 2/3` then
Construct any ΔABC. Construct ΔA'BC' such that AB : A'B = 5 : 3 and ΔABC ∼ ΔA'BC'.
