Advertisements
Advertisements
प्रश्न
दर्शाइए कि बिंदु A (a, b + c), B (b, c + a) और C (c, a + b) संरेख हैं।
उत्तर
ज्ञात है त्रिभुजों के शीर्ष A (a, b + c), B (b, c + a) और C (c, a + b)
`Delta` का क्षेत्रफल `= Delta = 1/2 abs (("x"_1,"y"_1,1),("x"_2,"y"_2,1),("x"_3,"y"_3,1))`
जहाँ, x1 = a,y1 = b + c, x2 = b, y2 = c + a, x3 = c, y3 = a + b
`= 1/2 abs (("a", "b + c", 1),("b", "c + a",1),("c", "a + b", 1)) ...("C"_1 -> "C"_1 + "C"_2)`
`= 1/2 abs (("a + b + c", "b + c", 1),("a + b + c", "c + a", 1),("a + b + c", "a + b", 1))`
`= 1/2 ("a + b + c") abs ((1, "b + c", 1),(1, "c + a", 1),(1, "a + b", 1))`
`= 1/2 ("a + b + c") xx 0 ...("C"_1 "तथा" "C"_2 "सामान है")`
`Delta` का क्षेत्रफल = 0
अत: बिंदु A, B, C संरेख हैं।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित प्रश्न में दिए गए शीर्ष बिंदुओं वाले त्रिभुजों का क्षेत्रफल ज्ञात कीजिए:
(1, 0), (6, 0), 4, 3)
निम्नलिखित प्रश्न में दिए गए शीर्ष बिंदुओं वाले त्रिभुजों का क्षेत्रफल ज्ञात कीजिए:
(2, 7), (1, 1), (10, 8)
निम्नलिखित प्रश्न में दिए गए शीर्ष बिंदुओं वाले त्रिभुजों का क्षेत्रफल ज्ञात कीजिए:
(-2, -3), (3, 2), (-1, – 8)
प्रश्न में k का मान ज्ञात कीजिए यदि त्रिभुजों का क्षेत्रफल 4 वर्ग इकाई है। जहाँ शीर्ष बिंदु निम्नलिखित हैं।
(k, 0), 4, 0), (0, 2)
प्रश्न में k का मान ज्ञात कीजिए यदि त्रिभुजों का क्षेत्रफल 4 वर्ग इकाई है। जहाँ शीर्ष बिंदु निम्नलिखित हैं।
(-2, 0), (0, 4), (0, k)
सारणिकों का प्रयोग करके (1, 2) और (3, 6) को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए।
सारणिकों का प्रयोग करके (3, 1) और (9, 3) को मिलाने वाली रेखा को समीकरण ज्ञात कीजिए।
यदि शीर्ष (2,-6), (5, 4) और (k, 4) वाले त्रिभुज का क्षेत्रफल 35 वर्ग इकाई हो तो k का मान है:
निम्न त्रिभुज का क्षेत्रफल ज्ञात कीजिए:

निम्न त्रिभुज का क्षेत्रफल ज्ञात कीजिए:

निम्न त्रिभुज का क्षेत्रफल ज्ञात कीजिए:
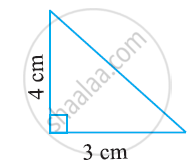
निम्न त्रिभुज का क्षेत्रफल ज्ञात कीजिए:
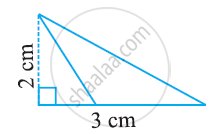
रिक्त स्थान का मान ज्ञात कीजिए:
| आधार | ऊँचाई | त्रिभुज का क्षेत्रफ़ल |
| 15 cm | ______ | 87 cm2 |
त्रिभुज ABC, A पर समकोण है (आकृति देखिए), और AD भुजा BC पर लंब है। यदि AB = 5cm, BC = 13 cm और AC = 12 cm है, तो ΔABC का क्षेत्रफल ज्ञात कीजिए। AD की लंबाई भी ज्ञात कीजिए।

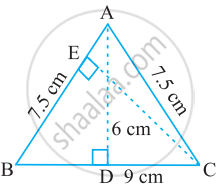
ΔABC समद्विबाहु त्रिभुज है जिसमें AB = AC = 7.5 cm और BC = 9 cm है (आकृति देखिए)। A से BC तक की ऊँचाई AD, 6 cm है। ΔABC का क्षेत्रफल ज्ञात कीजिए। C से AB तक की ऊँचाई, अर्थात CE क्या होगी?
रिक्त स्थान का मान ज्ञात कीजिए:
| आधार | ऊँचाई | त्रिभुज का क्षेत्रफ़ल |
| ______ | 31.4 mm | 1256 mm2 |
रिक्त स्थान का मान ज्ञात कीजिए:
| आधार | ऊँचाई | त्रिभुज का क्षेत्रफल |
| 22 cm | ______ | 170.5 cm2 |
