Question

एक चतुर्भुज की रचना की जा सकती है, यदि उसकी चारों भुजाएँ और एक विकर्ण दिया हो।

विकल्प

• सत्य

• असत्य

Answer 1

यह कथन सत्य है।

स्पष्टीकरण:

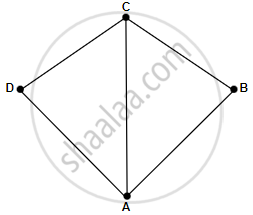
1. मान लीजिए AB, BC, CD, AD (भुजाएँ) और AC (विकर्ण) दिए हुए हैं।
2. SSS रचना का प्रयोग करके ∆ABC बनाइए।
3. अब, हमें चौथे बिंदु D का पता लगाना है। यह 'D' AC के सन्दर्भ में B के विपरीत दिशा में होगा।
4. इसलिए, A को केंद्र मानकर AD के बराबर लंबाई की त्रिज्या का एक चाप बनाएं।
5. अब, C को केंद्र मानकर CD के बराबर लंबाई की त्रिज्या का एक चाप बनाएं।
6. इन 2 चापों का प्रतिच्छेदन D है। D को चिह्नित करें और ABCD को पूरा करें।