Question

एक समांतर चतुर्भुज ABCD खींचिए, जिसमें BC = 5 cm, AB = 3 cm और ∠ABC = 60° है। विकर्ण BD द्वारा इसे दो त्रिभुजों BCD और ABD में विभाजित कीजिए। 

Answer 1

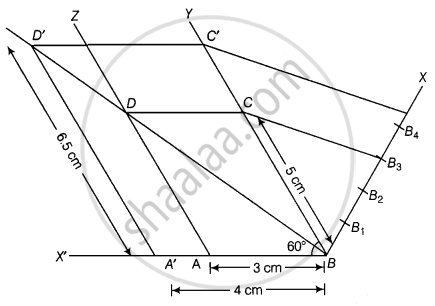
निर्माण के चरण:

1. एक रेखाखंड AB = 3 cm खींचिए।
2. अब, एक न्यून कोण ∠ABY = 60° बनाकर एक किरण खींचिए।
3. B को केंद्र मानकर और 5 cm त्रिज्या लेकर एक चाप लगाएं और BY पर बिंदु C को काटें।
4. फिर से एक किरण AZ खींचिए जिससे न्यून कोण ∠ZAX' = 60° हो। ...[∴ द्वारा || AZ, ∴ ∠YBX' = ZAX' = 60°]
5. A को केंद्र मानकर और 5 cm त्रिज्या लेकर एक चाप बनाएं और AZ पर बिंदु D काटें।
6. अब, CD को जोड़ें और अंत में एक समांतर चतुर्भुज ABCD बनाएं।
7. BD को मिलाएँ, जो समांतर चतुर्भुज ABCD का एक विकर्ण है।
8. B से कोई भी किरण BX नीचे की ओर खींचिए जिससे एक न्यून कोण ∠CBX बनता है।
9. BX पर 4 बिंदु B₁, B₂, B₃, B₄ इस प्रकार खोजें कि B₁ = B₁B₂ = B₂B₃ = B₃B₄।
10. B₄C को जोड़ें और B₃C से एक रेखा खींचें B₄C' || B₃C विस्तारित रेखा खंड BC को C' पर प्रतिच्छेद करता है।
11. बिंदु C' से खींचिए C'D' || CD विस्तारित रेखा खंड BD को D' पर प्रतिच्छेद करती है। फिर, AD'BC' आवश्यक त्रिभुज है जिसकी भुजाएँ ΔDBC की संगत भुजाओं की `4/3` हैं।
12. अब DA के समानांतर एक रेखा खंड D'A' खींचें, जहां A' विस्तारित भुजा BA यानी किरण BX' पर स्थित है।
13. अंत में, हम देखते हैं कि A'BCD' एक समांतर चतुर्भुज है जिसमें A'D' = 6.5 cm A'B = 4 cm और ∠A'BD' = 60° इसे त्रिभुज BC'D' और A'BD' में विभाजित करें विकर्ण BD।